Mutarotation - Online Tutor, Practice Problems & Exam Prep

Mutarotation is the process by which anomeric forms of sugars, such as alpha and beta D-glucopyranose, interconvert through hydrolysis and cyclization. This equilibrium results in a mixture of both forms, with distinct optical activities; the alpha anomer rotates light differently than the beta. Acid-catalyzed mechanisms involve protonation, formation of a double bond, and subsequent ring closure, leading to the final product. The equilibrium favors the beta form at approximately 64%, demonstrating the importance of stability in determining the predominant anomer in solution.

Mutorotation and Optical Activity

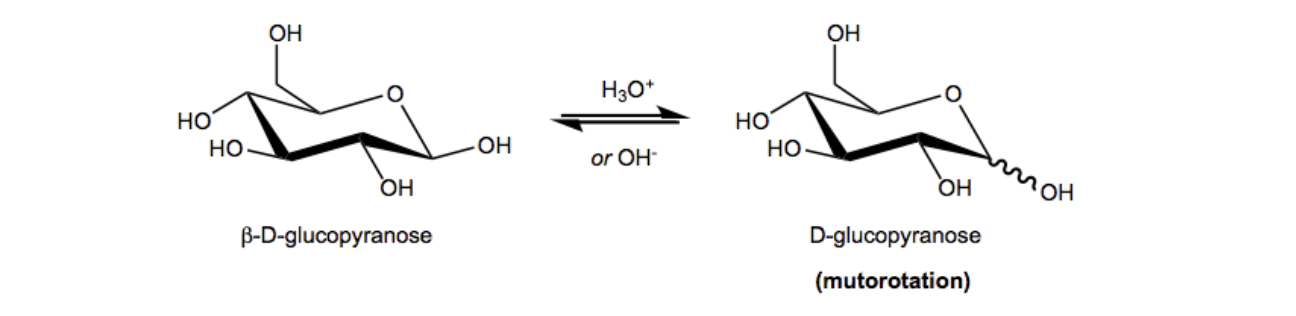
Now I want to dive deeper into the process by which an alpha anomer can become a beta anomer and so forth. So guys, pyranose and furanose rings are constantly hydrolyzing back and forth between their cyclic and straight-chain forms. Now you guys know what that mechanism looks like, you know what the rings look like, and I'm here to tell you that it's in constant equilibrium. It's not just like one ring gets formed then it stays like that; it's a constant equilibrium of hydrolysis, cyclization, decyclization, etc. Okay. Well, the specific process by which an anomeric position would convert between the alpha and beta forms is called mutarotation. It's basically the backward reaction of cyclization, but it's so that you can achieve the other anomer, okay? Now here in this example what I've done is I'm showing you how let's say you start off with a beta-D-glucopyranose and you expose it to either acid or to base, just a little bit of acid or just a little bit of base, this ring is going to start, is going to begin to hydrolyze and it's going to turn to the straight chain, and then it's going to eventually mutorotate forming the other anomer. Now what I did in this drawing is I didn't draw just the alpha anomer, I actually drew this squiggly line. What does that squiggly line mean? It means that you lose the alpha and beta anomer information because you're going to get some mixture of both. Now it's important to note, this is not going to be a racemate. Remember what racemate means? It means that you're going to get 50 of 50 of each. I'm not saying that, that's not what the squiggly line means here. It just means you're going to get a combination. So here instead of putting beta-D-glucopyranose, I just put D-glucopyranose because you're going to get a mixture of the two. Mutarotation is going to make it so that you're just going to have some kind of mixture of the two.

So guys, it turns out that in your textbook, the explanation of mutarotation is very, very closely tied with this idea of optical activity. So what I want to do is instead of having you read that and be confused, I just want to explain it so you can understand why they always talk about optical activity when they talk about mutarotation. And what it is is that optical activity provided the proof for mutarotation, which I'm going to show you now. So first of all, it's important to note that anomers always differ in optical activity. Okay. You're always looking α anomer is always going to rotate light differently than a β anomer, okay. For example, the alpha anomer of D-glucopyranose rotates light at a positive 112 rotation in a polarimeter okay. Whereas a beta-D-glucopyranose rotates light at around positive 19. Okay, guys these are super random numbers that you do not need to memorize, Okay? But this just shows you the completely different optical activity of the alpha versus the beta. Now if you weren't paying attention and maybe you just kind of thought very quickly, you might think, you might wonder why are they not just opposite rotations. Because remember that back when we talked about optical activity a long time ago, we talked about how if one enantiomer shows the positive rotation, the opposite enantiomer should then show the negative rotation of that same rotation of plain polarized light. In this case, they're both positive and they're very different from each other. Why is that? Well, guys, remember that anomers are not enantiomers of each other. Right? They're not enantiomers. Like a bunch of the chiral centers stayed the same. What they actually are is remember they're diastereomers. Okay. So that's why they have unrelated activities. You can't predict that one is going to be positive and one is going to be negative. They just have random numbers. Here I've given you the random numbers for glucopyranose, pyranose, but other types of rings, you would need to actually use a polarimeter to get that number. Okay? So it's not something that you're supposed to memorize.

Now why is this important? Well because back in the day when they were first discovering kind of this relationship between optical activity and chirality, it was noticed that D-glucopyranose always equilibrated to a positive 52.5 rotation, which is weird because that's not the rotation of either one of these right? 112 is one, the other one is 18.7 and somehow it would always rest if you let it sit around long enough, no matter which one you started with. Whether you started with 100% of the A or whether you started off with 100% of the B, they would always end up at a positive 52.5. Now this is strange because this is not even the midpoint, this is not even the halfway point of rotation between the two optical activities. So what I actually did is I made a little graph for you guys so you guys can really understand this. So notice that the beta had a rotation of positive 18 right and the alpha had a rotation of positive 112 right? So that means at the very beginning, let's say that we started off with a 100% of the beta anomer. Well, that would give us 18.7 optical activity. But what was noticed is that after several days of it being sitting in an aqueous solution, the optical activity would get more and more and more positive until it reached this magical number of 52.5. Now why is that? And then the same thing happened with this guy, with the alpha. The alpha would get lower and lower until it got to 52.5. Well, guys, the reason is because we learned, remember that we learned that specifically for beta-glucopyranose, the beta prevails at a 64% equilibrium and the alpha prevails at a 36% equilibrium, meaning that if you were to just start with one of them and allow it to mutarotate, you're eventually going to reach an equilibrium where 64% of the pyranose is in the beta form and 36% is in the alpha form. And that is why at the end, the rotation that you end up getting is 52.5 because that happens to be right at the 64% mark of the difference between the two. What this shows is that 64% of it is the beta and only 36% of it is the alpha. If it had been 50/50, let's say that it equilibrated to exactly 50/50, then we would expect a rotation right in the middle of these two, which is positive 65, but we don't see positive 65. What we see is that it's a little bit more than 60, it's a little bit less than 65, which must mean that the one that's on that side is the majority because it's the one with the lower optical activity and when you actually do the numbers, it shows that 64% is equal to the beta. Okay? So anyway, this is proof that mutarotation was occurring. You know, chemists back in the day, they realized oh, this must mean that, this must mean that if I have an alpha somehow it's going to equilibrate and become a beta. So then they started figuring out well what is a potential mechanism for this to take place? How could an alpha potentially become a beta? Well, that's going to be the next video. So hopefully this makes sense so far in terms of optical activity proving that mutarotation exists, and in the next video, I want to go into the mechanism.

Mechanism

Alright guys, so while mineral rotation is possible in both acid and base, I'm only going to show you the acid-catalyzed mechanism. And that's because it turns out that the base-catalyzed mechanism has a bunch of cross-reactions that are possible, which complicate the products. So usually, this is just shown in acid. Okay? So let's go ahead and get started. The very first step is protonation, as with any acid-catalyzed mechanism. So I'm just going to redraw my hydronium, so I can have one accessible proton and the protonated O will be the O in the ring because remember we need to break this ring somehow. Okay. So what this is going to do is it's going to give me a positively charged O, and at this point, I can use the electrons from my anomeric oxygen, remember that's the one we're trying to flip up and down to make a double bond. Okay, so two electrons from my O can come down and make a double bond, and then I can break this bond in the ring to form an alcohol. So at this point, what's going to happen is that the chirality of this carbon is now lost because it turned into a double bond which means it's trigonal planar now. It could be up or it could be down. Okay? Also, this O is going to have a positive charge because it still has an H. Cool? Awesome. So now guys we're just going to start doing the reverse and get rid of that double bond. So this O can now reform the ring, kicking electrons back up. So what this is going to do is it's going to give me once again a positive O. And now I'm going to get the other O. Now we're going to show that now it shifted to the up instead of down, and that's because this O could attack from either the top or the bottom. So it could make the O go up, or it could make it go down. In this case, since we started from the down position, I'm trying to rotate it, mutarotate it to the up position. So that's why I draw it up here. And then finally, guys, all we have to do is deprotonate. So then deprotonate so we can regenerate that catalytic acid, and we're going to go ahead and achieve a final product, which is now a β-D-glucopyranose. Okay? And oh, I'm sorry. Pyranose. And this is the process that turns this is the mutarotation process that turns an α to a β, and this is what's constantly taking place and eventually, they would reach equilibrium based on the stabilities of each. We know that for glucose it happens to be 64% of the β, but if this was any other sugar the number would be of the β, but if this was any other sugar the number would be different and the anomer might even be different, maybe the α would be favored with another sugar. Okay? Awesome guys, great job. Let's move on.

Here’s what students ask on this topic:

What is mutarotation in carbohydrates?

Mutarotation is the process by which the alpha and beta anomeric forms of sugars, such as D-glucopyranose, interconvert in aqueous solution. This occurs through the hydrolysis of the cyclic form to the open-chain form, followed by re-cyclization. The equilibrium between these forms results in a mixture of both anomers, each with distinct optical activities. For example, alpha-D-glucopyranose and beta-D-glucopyranose rotate plane-polarized light differently. The equilibrium typically favors one anomer over the other, such as the beta form being more prevalent at approximately 64% in the case of glucose.

How does mutarotation affect optical activity?

Mutarotation affects optical activity by causing a change in the rotation of plane-polarized light as the equilibrium between alpha and beta anomers shifts. Each anomer has a distinct optical rotation; for instance, alpha-D-glucopyranose has a rotation of +112°, while beta-D-glucopyranose has a rotation of +19°. When mutarotation occurs, the solution reaches an equilibrium mixture of these anomers, resulting in an overall optical rotation that is a weighted average of the individual rotations. For glucose, this equilibrium rotation is +52.5°, reflecting the predominance of the beta form at 64%.

What is the mechanism of acid-catalyzed mutarotation?

The acid-catalyzed mechanism of mutarotation involves several steps. First, protonation of the oxygen in the ring occurs, making it positively charged. This facilitates the breaking of the ring and formation of a double bond, resulting in a planar, achiral intermediate. The ring can then re-close, with the hydroxyl group attacking from either the top or bottom, leading to the formation of either the alpha or beta anomer. Finally, deprotonation occurs, regenerating the catalytic acid and completing the process. This mechanism allows for the interconversion between alpha and beta forms, eventually reaching an equilibrium based on their relative stabilities.

Why does glucose favor the beta anomer in equilibrium?

Glucose favors the beta anomer in equilibrium due to the relative stability of the beta form compared to the alpha form. In the beta-D-glucopyranose, the hydroxyl group at the anomeric carbon is in the equatorial position, which is sterically more favorable and less hindered than the axial position in the alpha-D-glucopyranose. This reduced steric hindrance makes the beta form more stable, leading to its predominance at approximately 64% in equilibrium. The specific optical rotation of the equilibrium mixture, +52.5°, reflects this higher proportion of the beta anomer.

Can mutarotation occur in both acidic and basic conditions?

Yes, mutarotation can occur in both acidic and basic conditions. However, the mechanisms differ. In acidic conditions, the process involves protonation, ring opening, and re-cyclization, as described in the acid-catalyzed mechanism. In basic conditions, the mechanism is more complex due to potential cross-reactions that can complicate the products. Despite these differences, both conditions facilitate the interconversion between alpha and beta anomers, leading to an equilibrium mixture. Typically, the acid-catalyzed mechanism is more commonly discussed due to its relative simplicity and fewer side reactions.