Perfect Competition Profit on the Graph - Online Tutor, Practice Problems & Exam Prep

To maximize profit, firms produce where marginal revenue equals marginal cost. This point indicates the optimal quantity, which can also minimize losses. Profit is calculated using the formula: (Price-Average Total Cost)⁢Quantity. If price exceeds average total cost, profit occurs; if not, losses arise. Understanding these concepts is crucial for analyzing market structures and making informed production decisions in economics.

Profit on the Graph in Perfect Competition

Alright, now let's see how we find the profit-maximizing quantity, right? Where we want to produce as well as how we calculate profit on the graph. Let's do that now. So the profit-maximizing quantity, right? Even in the very first lesson we did, I mentioned where we're going to produce, right? And we talked about this key formula about marginal benefits and marginal costs, right? To the firm, marginal benefits are the marginal revenues, right? The money that they're bringing in, and the marginal cost, well, that's the cost, right? The extra money they're going to spend to earn that revenue. So here we go, the profit-maximizing quantity is where that marginal revenue equals the marginal cost. Okay? And now one thing to note is that profit-maximizing could also mean loss minimizing, right? It doesn't necessarily mean that we're going to make money, but at least we're going to lose as little money as possible, right? So marginal revenue equals marginal cost, that is the key point on our graph. We're always going to be looking for this point pretty much every time we go to the graph this is going to be a point we're looking for. Alright, so let's go ahead and find that on this graph right now. We're given the price on the market, right? We saw that the price for a bushel of wheat was $4 so the firm is going to face this flat demand curve and we did say that, the price, right, is going to equal that average revenue and it's going to equal the marginal revenue in perfect competition, right? So there we go. We've got our marginal revenue curve right there which is equal to the demand curve for the firm, this is the demand curve for the firm and there we go. We've got a marginal cost curve there as well given to us and we're going to find our profit-maximizing quantity. So we just have to find where these curves cross, which is very simple right here and this is the profit-maximizing quantity. We got to see how much quantity would we produce at this point. Well it would be right here like 4.5 and let's say just for a hypothetical, let's say it was a case that you can't produce 4.5 bushels, right? You can't do like half a bushel of wheat, well what would you do? Would you produce 4 or would you produce 5? What do you think in this case? So look at the graph right here and think of what happens if we produce 4 units and think of what happens if we produce 5. If we produce 4 units, well we're right here, right? We would be producing here, we would be bringing in this much revenue and it would cost us this much, right? So the cost is still less than the revenue. That's a good thing, but if we produce 5, notice what happens. Now the cost is above the revenue. That's a bad thing, right? We don't want the cost for it to cost more than the money we bring in. So in that hypothetical case where you got to pick one or the other, you're going to pick the lower one, right? Because if we went up to 5, we would lose some money and we wouldn't maximize profit. So ideally, we would go right here where the lines cross and that's what you're usually going to see pretty much in all the problems there, you're not going to have to deal with this, but I'm just throwing it out there as just an intuitive thing, right? Right? We're going to produce just a little less if we have to, right? We never want that marginal cost to be greater than our marginal revenue. Alright, so right there is where we would want to produce at 4.5 units ideally, so let's go ahead and discuss how we're going to calculate the profit or the loss based on this quantity. We know that we want to produce this quantity, how much money is that going to make us? How do we calculate that? Well let's go on down here. So we've got our formula for profit first here in the middle of the screen and what we've got is the price minus the average total cost, alright? So now we're going to bring in another curve into the whole mix here. We've been dealing with marginal revenue and marginal cost so far and now we're going to deal with average total cost as well. Okay? So that price minus the average total cost, this bracket right here, this parenthesis, that's the profit per unit, right? If we take the price, that's the money we're going to bring in for the unit minus the average total cost, that's what it costs us for that unit times the quantity, okay? So that's kind of just a very general profit formula and it's going to work in all market structures. We're going to keep this formula throughout the next several chapters. Price minus average total cost in parenthesis to get our profit per unit and then we multiply that by quantity. Okay? So let's go ahead down to these two graphs down here knowing what we know about profit now and let's use these 2 steps. These 2 steps are always going to be relevant when we're trying to calculate profit, okay? This is going to work in other market structures as well, so let's go ahead and start here with finding the profit-maximizing quantity, right right? That's always going to be the first step. How much are we going to produce and then we're going to calculate the profit, okay? So the first step, how much are we going to produce? We need to find where marginal revenue and marginal cost curves intersect. Okay? So let's start here on this left graph. So find your marginal revenue curve, your marginal cost curve, and mark the point where we're going to produce. Alright? I'll give you a second to try it and then I'm going to mark it. So right here, right, we've got our marginal revenue, the flat demand curve, right, which is also our marginal revenue curve in perfect competition, crossing the marginal cost curve right there. Right? So if we go down to our quantity axis, right, just like we're used to a quantity axis here, a price. Now we're going to extend this axis a little bit at this point because it's not just prices that go on this up down axis now, it's also cost as well, so it's going to be prices, costs, it's just dollar values, okay? So the idea here is that these are really just dollar values because we're going to have prices like the price of the product that we see here in the middle, but it also shows cost like we have on these cost curves. So it's just a little better I guess nomenclature to use a whole just wider range, right? Just to say dollars on that axis. Okay. So back to the point here. We've got our marginal revenue and our marginal cost. We found the point where we're going to produce and we need to find out what quantity that's going to be. So we're going to take it down to the quantity axis and it'll be this quantity right here, right? That would be the quantity that we're going to produce and maximize our profit. Okay, so now how do we calculate the profit? So it tells us we're going to find the price which is on the demand curve, right? The price is always going to be on the demand curve. Average revenue, which is price, equals our demand curve. Every market structure is like that. Okay? Now in this one it's easy because the price it's the same spot as the marginal revenue. It'll get a little more complicated in other market structures, but right now it's easy, right? We've got our price, on the demand curve at that point is right there, right here in the same dot and we want to find at that same quantity what our average total cost is. So if this is our price, then we've got our average total cost right here, right? This is our average total cost at that quantity. Well, the price minus the average total cost, right? If price so let's say I'm going to do this a little visual example for you here. So the price would be this whole line, right? So I'm going to do it off to the side. The price would have been this whole line right here, right? And the average total cost was this whole area right here, right? This area. I'm doing it off to the side, but I'm talking about that quantity, right? That profit-maximizing quantity. So if that whole blue line was the price and the green area I shaded is the average total cost, what's left over here, this little area right here, that's the profit per unit, right? So that profit is going to be this line right here between the marginal revenue curve or excuse me the price, right, and the average total cost and we multiply it by the quantity, okay? So the quantity over here, we're going to get that this whole region right here is our profit, right? So we want to find the price and the average total cost at our profit-maximizing quantity and then that is going to be our profit right there, that area. Okay. So this is our profit right here, okay? And that's because the average total cost was less than the price, right? At that quantity, our average total cost was less than price, so we made profit here. I'm going to label it here at the top as profit in this case, right? Because our average total cost was less than the price. Now how about on this right-hand graph? Look how high up that average total cost curve has become, right? So let me go ahead and get out of the way so we can see the whole graph and let's do the same thing, right? Remember, we always start by finding marginal revenue equaling marginal cost. Well, where's our marginal revenue curve? Where's our marginal cost curve? Go ahead and mark the point. I'm going to give you a few seconds and then I'm going to mark it. Alright, so our profit-maximizing quantity will be where this marginal revenue equals marginal cost right here. Okay? So our profit-maximizing quantity in this case is right here, Q, okay? Now our second step right, we need to find price and average total cost at this quantity. So in perfect competition, it's easy because the price is right there on the same dot that we already picked and our average total cost at that quantity is right up here, right? So notice what's happened this time. Now the average total cost is greater than the price at the profit-maximizing quantity. So this actually becomes a loss-minimizing quantity, right? So this is still where we're going to want to produce to minimize our loss. Okay? So the same thing's going to happen. We're going to take the space right between the 2, Right? This area or this line right here represents the loss per unit times all the units that we sell. Right? We're going to sell all these units here and that's going to be the loss is going to be this box that I just shaded in, alright? So that is the amount of our loss. We could calculate that if we had a number for our quantity, a number for our price and average total cost, we could calculate the area of that rectangle, right? So that would be the loss-minimizing quantity, right? If we tried any other point, we would increase the loss, All right. So let's go ahead and make some conclusions here about what we've seen. So let's go ahead well first let's label this graph. This was the loss graph on the right-hand side, right. That was a loss that we just illustrated, so let's go ahead and make these conclusions down here. If price is greater than average total cost, just like we saw in that left graph, right, the price was greater than average total cost, well there we're going to make profit, right? Let's go on to the right hand side behind me. Let me get it back out of the way. Price less than average total cost. So like we saw in the right graph, right? The average total cost was above the price. Well, we had a loss in that case and how about in the middle when the price equals the average total cost? Well, if you think about that on our profit right here, if this equals this, right, price equals average total cost 5 if the price is 5 and average total cost is 5, 5 minus 5 is 0, right? So we're going to end up with 0. No profit and no loss. If p equals ATC, we're going to say we break even. Okay? We don't make a profit and we don't make a loss. Alright, so this is how we're going to see the profit and loss on the graph, right? So you should be ready to find these key points on the graph and calculate profit and loss after this lesson. Alright, so easy steps. First, we're going to find that marginal revenue equals the marginal cost and then we take it to the price and the average total cost to calculate our profit or loss. Alright, let's go ahead and practice a little bit before we move on to the next topic. Alright, let's do that in the next video.

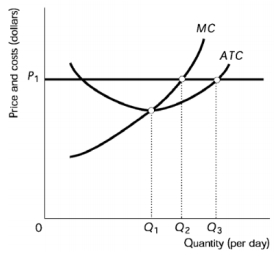
If the firm decreases its production from Q2 to Q1, it will 

• A. Increase its profit
• B. Decrease its profit
• C. Reduce its marginal revenue
• D. Increase its marginal revenue

If the price is P1, the firm maximizes profit by producing 

• A. Q1
• B. Q2
• C. Q3
• D. Nothing

If the price is P1, the firm is 

• A. Suffering an economic loss
• B. Earning an economic profit
• C. Breaking even
• D. None of the above

Here’s what students ask on this topic:

What is the profit-maximizing quantity in perfect competition?

The profit-maximizing quantity in perfect competition is where the marginal revenue (MR) equals the marginal cost (MC). This point indicates the optimal quantity of output that a firm should produce to maximize its profit or minimize its losses. In perfect competition, the price (P) is equal to the marginal revenue, so the firm will produce where P = MC. This ensures that the additional revenue from selling one more unit equals the additional cost of producing that unit, optimizing the firm's profit.

How do you calculate profit on a graph in perfect competition?

To calculate profit on a graph in perfect competition, follow these steps: First, identify the profit-maximizing quantity where marginal revenue (MR) equals marginal cost (MC). Next, find the price (P) on the demand curve at this quantity. Then, determine the average total cost (ATC) at the same quantity. Profit per unit is calculated as (P - ATC). Multiply this by the quantity to get total profit. The formula is: $(P-\mathrm{ATC})Q$.

What happens if the price is less than the average total cost in perfect competition?

If the price (P) is less than the average total cost (ATC) in perfect competition, the firm incurs a loss. This is because the revenue from selling each unit is not enough to cover the cost of producing it. The loss per unit is calculated as (ATC - P). The total loss is this amount multiplied by the quantity produced. The firm will still produce where marginal revenue (MR) equals marginal cost (MC) to minimize its losses, even if it cannot make a profit.

How do you find the average total cost on a graph in perfect competition?

To find the average total cost (ATC) on a graph in perfect competition, first identify the profit-maximizing quantity where marginal revenue (MR) equals marginal cost (MC). Then, locate the ATC curve at this quantity. The point where the ATC curve intersects the vertical line drawn from the profit-maximizing quantity on the horizontal axis gives the ATC. This value represents the cost per unit of output at the optimal production level.

What is the significance of the point where marginal revenue equals marginal cost?

The point where marginal revenue (MR) equals marginal cost (MC) is significant because it represents the profit-maximizing or loss-minimizing quantity of output for a firm. At this point, the additional revenue from selling one more unit equals the additional cost of producing that unit. Producing beyond this point would result in higher costs than revenue, reducing profit. Conversely, producing less would mean not fully capitalizing on potential profit. This principle is crucial for making informed production decisions in economics.

How do you determine if a firm is making a profit or a loss in perfect competition?

To determine if a firm is making a profit or a loss in perfect competition, compare the price (P) to the average total cost (ATC) at the profit-maximizing quantity. If P > ATC, the firm makes a profit. If P < ATC, the firm incurs a loss. If P = ATC, the firm breaks even, making neither profit nor loss. This comparison helps assess the firm's financial performance and guides production decisions.