Two patterns of packing for two different circles of the same size are shown here. For each structure (b) determine the angle between the lattice vectors, g, and determine whether the lattice vectors are of the same length or of different lengths; (i)

(ii)

Key Concepts

Lattice Vectors

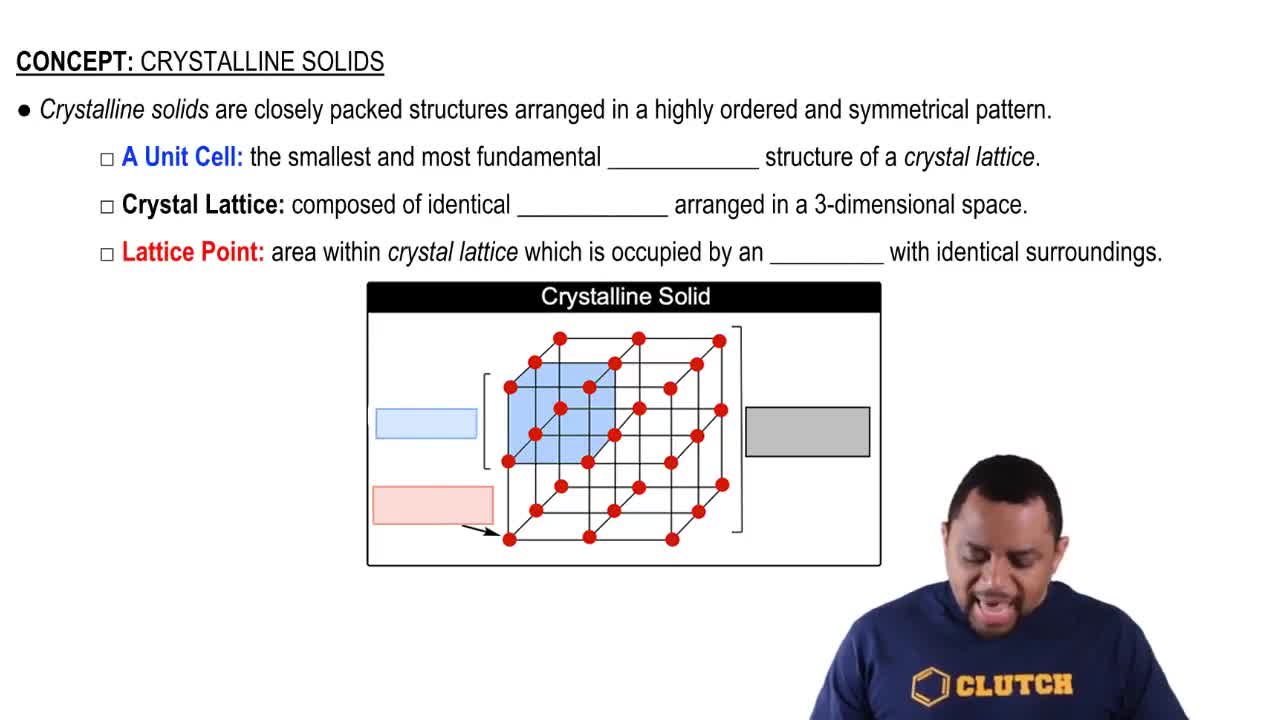
Lattice vectors are the fundamental building blocks of a crystal lattice, defining the periodic arrangement of points in space. They are represented as vectors that connect points in the lattice, and their lengths and angles determine the symmetry and structure of the crystal. In the context of the question, analyzing the lengths and angles of the lattice vectors helps identify the packing arrangement of the circles.

Crystalline Structures

Crystalline structures are ordered arrangements of atoms, ions, or molecules in a solid, characterized by repeating patterns. The two packing patterns shown in the image represent different crystalline arrangements, which can affect properties such as density and stability. Understanding these structures is essential for determining the angles and lengths of the lattice vectors in the given question.

Angle Between Lattice Vectors

The angle between lattice vectors is a critical parameter that influences the geometry of the crystal lattice. It can indicate the type of packing arrangement, such as square or hexagonal packing, and is essential for understanding the spatial relationships between the particles in the lattice. In the question, calculating this angle is necessary to differentiate between the two packing patterns presented.