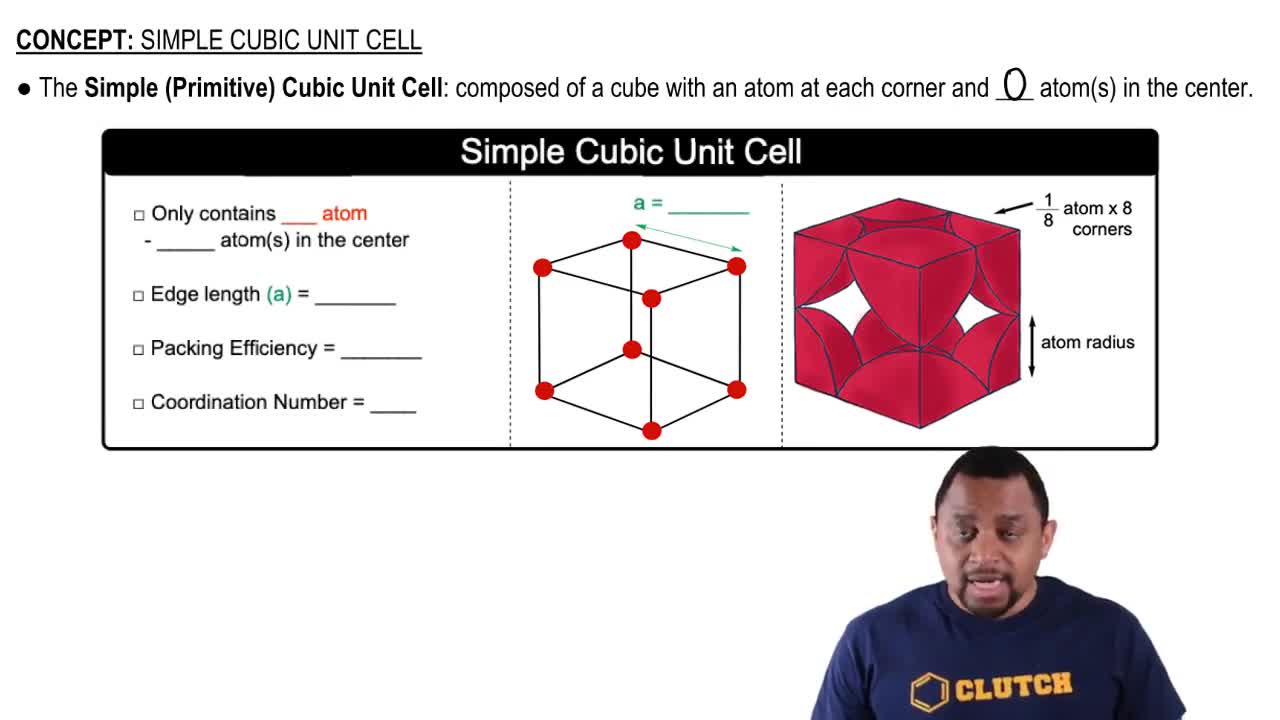
Here are the essential concepts you must grasp in order to answer the question correctly.
Primitive Lattices
Primitive lattices are the simplest repeating units in a crystal structure, defined by their unit cells. These unit cells can vary in shape and size, and they are characterized by their lattice parameters, which include the lengths of the edges and the angles between them. Understanding the types of primitive lattices is essential for identifying their geometric properties.
Recommended video:
Unit Cell Angles
The angles between the edges of a unit cell are crucial for classifying crystal systems. In three-dimensional lattices, the internal angles can be 90 degrees or vary, leading to different classifications such as orthorhombic (all angles 90°) or triclinic (no angles 90°). Recognizing these angles helps in determining the symmetry and properties of the crystal structure.
Recommended video:
Crystal Systems
Crystal systems categorize crystals based on their symmetry and lattice parameters. There are seven primary crystal systems, including triclinic and rhombohedral, which are characterized by their unique angles and edge lengths. Understanding these systems is vital for identifying which lattices have non-right angles and for solving related crystallography problems.
Recommended video: