Textbook Question
(b) Now draw a picture that represents an amorphous solid at the atomic level.
685
views

 Verified step by step guidance
Verified step by step guidance


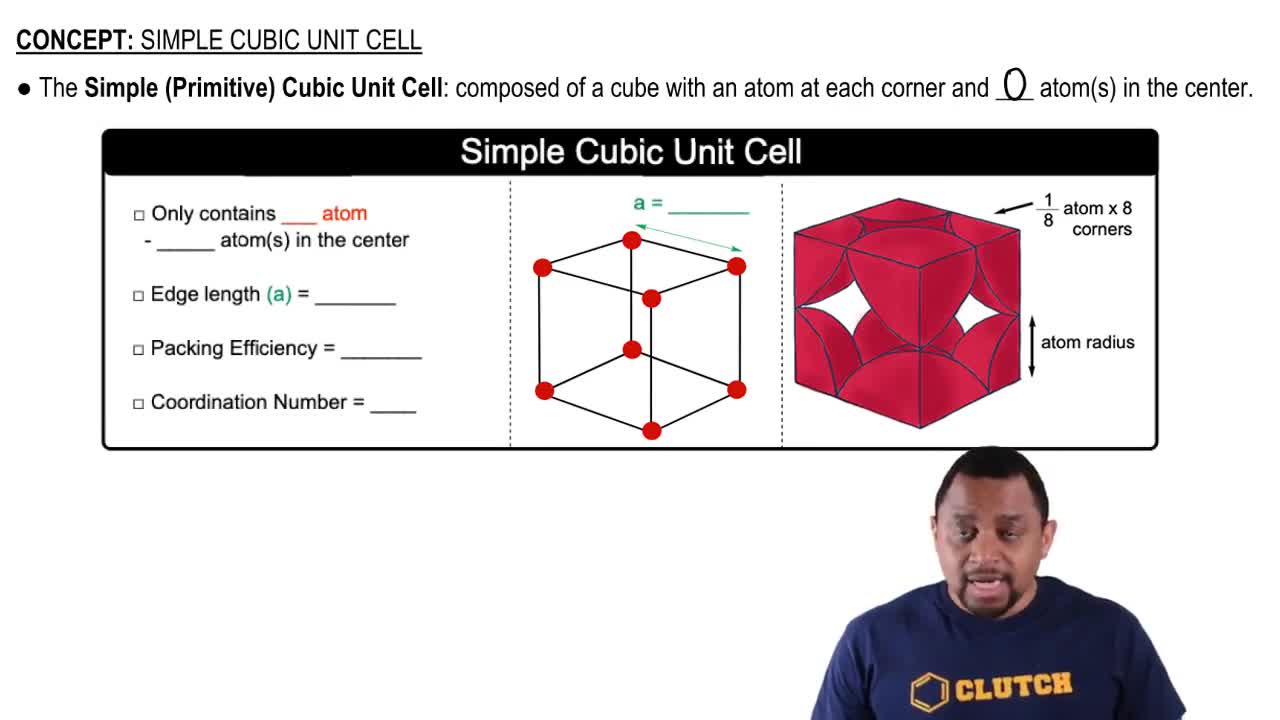
(b) Now draw a picture that represents an amorphous solid at the atomic level.
Two patterns of packing for two different circles of the same size are shown here. For each structure (b) determine the angle between the lattice vectors, g, and determine whether the lattice vectors are of the same length or of different lengths; (i)
(ii)
Two patterns of packing two different circles of the same size are shown here. For each structure (c) determine the type of two-dimensional lattice (from Figure 12.4). (i)
(ii)
Which of the three-dimensional primitive lattices has a unit cell where none of the internal angles is 90? (a) Orthorhombic, (b) hexagonal, (c) rhombohedral, (d) triclinic, (e) both rhombohedral and triclinic.