Here are the essential concepts you must grasp in order to answer the question correctly.
Focal Length
The focal length of a lens is the distance from the lens at which parallel rays of light converge or appear to diverge. For a simple magnifier, a positive focal length indicates that it is a converging lens. The focal length is crucial for determining how the lens will magnify an object and is typically measured in centimeters.
Recommended video:
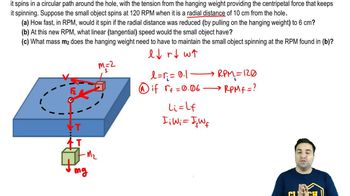
Spinning on a string of variable length
Magnification
Magnification is the ratio of the height of the image formed by a lens to the height of the object. It can be calculated using the formula: Magnification (M) = Image Height (h') / Object Height (h). In the case of a magnifier, a higher magnification means a larger image, which is essential for understanding how the lens enhances the visibility of small objects.
Recommended video:
Thin Lens Formula
The thin lens formula relates the object distance (u), image distance (v), and focal length (f) of a lens: 1/f = 1/v + 1/u. This formula is fundamental in optics for determining the position and size of the image formed by a lens. It helps in calculating the image height when the object height and focal length are known.
Recommended video: