A rifle is aimed horizontally at a target 50 m away. The bullet hits the target 2.0 cm below the aim point. (b) What was the bullet's speed as it left the barrel?

Verified step by step guidance

1. Step 1: Identify the known values from the problem. The horizontal distance to the target is 50 m, the vertical displacement of the bullet is 2.0 cm (convert to meters: 0.020 m), and the acceleration due to gravity is approximately 9.8 m/s². The bullet's initial vertical velocity is 0 m/s since it is fired horizontally.
2. Step 2: Use the vertical motion equation to determine the time it took for the bullet to fall 2.0 cm. The equation for vertical displacement is: $y=\frac{1}{2}g{t}^2$, where $y$ is the vertical displacement, $g$ is the acceleration due to gravity, and $t$ is the time. Rearrange the equation to solve for $t$: $t=\sqrt{\frac{2}{g}y}$.
3. Step 3: Substitute the known values into the rearranged equation to calculate the time of flight. Use $y=\; 0.020$ m and $g=\; 9.8$ m/s².
4. Step 4: Use the horizontal motion equation to find the bullet's speed. The equation for horizontal motion is: $x=vt$, where $x$ is the horizontal distance, $v$ is the horizontal velocity, and $t$ is the time. Rearrange the equation to solve for $v$: $v=\frac{x}{t}$.
5. Step 5: Substitute the known values into the rearranged equation for horizontal velocity. Use $x=\; 50$ m and the time calculated in Step 3 to find the bullet's speed as it left the barrel.

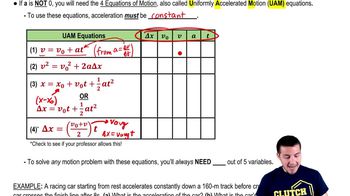
Key Concepts

Projectile Motion

Projectile motion refers to the motion of an object that is launched into the air and is subject to gravitational forces. In this scenario, the bullet follows a parabolic trajectory due to gravity acting on it after being fired horizontally. Understanding the principles of projectile motion is essential to analyze how the bullet travels and falls below the aim point.

Kinematic Equations

Kinematic equations describe the motion of objects under constant acceleration. In this case, the vertical displacement of the bullet can be calculated using the equation for vertical motion, which relates distance, initial velocity, acceleration due to gravity, and time. These equations allow us to determine how long the bullet was in the air, which is crucial for finding its horizontal speed.

Horizontal Velocity

Horizontal velocity is the speed at which an object moves along the horizontal axis. For the bullet, this velocity remains constant since there are no horizontal forces acting on it after it leaves the barrel. By calculating the time the bullet is in the air and knowing the horizontal distance to the target, we can determine the bullet's speed as it left the barrel.