Rate Law - Online Tutor, Practice Problems & Exam Prep

The rate law is an essential concept in chemistry that establishes the relationship between the rate of a chemical reaction and the concentrations of reactants. It is expressed as:

$\mathrm{rate}=k{\left[A\right]}^x{\left[B\right]}^y$

where k represents the rate constant, A and B are the reactant concentrations, and x and y are their respective reaction orders. Reaction orders are determined through experimentation or reaction mechanisms and are crucial in calculating the overall rate of a reaction. The rate law focuses solely on reactants, disregarding product concentrations. To find the units for the rate constant (k), one must calculate the overall order (n) by summing all individual reaction orders and using the formula:

$k=M^{(1-n)}\cdot {\mathrm{time}}^{(-1)}$

When solving rate law problems, it's imperative to first determine reaction orders before calculating the rate constant and the new rate, following a systematic approach to ensure accuracy.

Rate Law Concept 1

Now the rate law is just an expression that relates the rate of a reaction to its react, change of reacting concentrations, rate constant and reaction orders. Now your rate constant is a proportionality constant that links the rate to these reactant concentrations, and your reaction orders well. These are just the exponent component for the given concentrations. Now they're determined mathematically with a chart which has given values or from a series of steps called a reaction mechanism.

Here we're not going to go into detail on reaction mechanisms just yet because pretty abstract. Later on we'll go in greater detail on what reaction mechanisms are and how we can use them to figure out our reaction orders. Now also what's important is that rate law ignores products because notice I only talked about the concentration of the reactants. I never mentioned concentrations of products because when it comes to rate law we ignore products altogether.

Now our rate law has its rate law expression which is rate equals K which is your rate constant times AXBY. Now A & B represent your reaction concentration or reactant concentrations. Here, if your chemical equation had more than two reactants then we continue we'd have CZ X and Y. These are your exponents or reaction orders. So just remember, your rate law is trying to connect the ideas of changes in concentration for your reactants, rate constant and reaction orders in order to find the overall rate of any given chemical reaction.

Rate Law Example 1

The chemical reaction has a rate law of KA3B1C0. By what factor would the rate increase if the concentration of A were tripled, the concentration of B was cut by half, and the concentration of C was increased by half, and the ray constant K was kept constant. All right. So here we're going to say rate equals KA3B1C0. They're telling me that our rate constant case staying the same, it's not changing, so it's not going to affect any change in rate. So we can ignore it for now.

And here we're talking about tripling, cutting in half, increasing by half each one of these reactant concentrations to make it easy for us. They don't give us their initial amounts, so just make them all one molar, OK, just to make it easy because proportionally it wouldn't matter. I can make them all three molar doing what it tells me to do, I'd still get the same answer. So here we're going to assume that they're all starting at one molar, and here I'm going to AAA. So it's going to go from one molar to three molar and it's still to the 3B is getting cut by half.

So you start at one molar and you cut it by half. So now you only have 0.5 left still to the one and C we're still going to do C, but it's not going to really matter. We're increasing it by half, so now it becomes 1.5 C really doesn't matter because any number to the zeroth power is equal to 1. So I could make this concentration inside. For CA million it won't matter because a million to zero is still equal to 1. So really all that is important to figure out. The change in rate is A&B, so 33 is 27 * 5 is 13.5.

This means that my rate would be expected to increase by 13.5 fold. This is how much faster my rate would go, because increasing the concentration of my reactants would cause an increase in the rate. Here we're seeing it mathematically being shown to us O. Here option C would be the correct answer.

Rate Law Concept 2

Now the units for the ray constant K can be determined by first calculating the overall order. Now our overall order uses the variable N. It's a numerical value calculated from the addition of all reaction orders and here the formula to figure out the units for your ray constant.

K is K = m 2 N + 1 × time ⁻ 1 . So remember K is your weight constant capital, M is your molarity, and N again is your overall order. So adding up all the orders of your rate law helps you to figure out N. Take that and plug it into this formula and you'll know what the units for K will be.

Rate Law Example 2

What is the overall order and the units for the rate constant K for the following chemical reaction shown below that has a rate equal to K NL₂ to the two, CL₂ to the one. All right, so remember two and one are your reaction orders. To find your overall order you just add them together. So this would be 2 + 1. So your reaction would be third order overall.

Now for K we'd say. Remember K is M to the negative N + 1 times time. Inverse here. Time could be in units of seconds, minutes, gears, whatever. So this would be M to the -3 + 1. Here. Let's just say seconds are the units of time that we're looking at, and so this would be M to the -2 times seconds inverse.

So whatever the actual value of K would be, these would be the units that follow it. So it would be some value M to the -2 * s to the -1. So we'd be third order overall and these would be the units for our rate constant K.

Rate Law Concept 3

The rate constant and reaction orders of the rate law are determined mathematically when given our reactant concentrations and initial rates. Now this is the sequence that you have to use in order to solve all of the components of the write log. The first thing that we can solve are our reaction orders.

So now once you have your reaction orders determined, you can use that information to determine your rate constant K, and then once you have that, you can then determine your new rate. So if you're given a question where they're giving you information on the reacting, concentration, and initial rates, and they want you to find your rate constant K, you can't just skip to rate constant K. You have to first find your reaction orders.

Once you do that, then you can find K. If they give you reacting concentrations and initial rates and ask you to find your new rate, you can't just skip all the way to new rate. You have to do reaction orders to find your rate constant and then you can find your new rate. So keep this in mind anytime we're asked to deal with any calculations dealing with rate law determination.

Rate Law Example 3

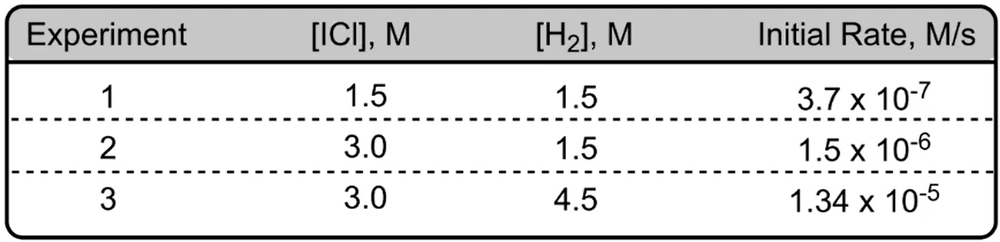
The initial rates of reaction 2 NO gas + Cl₂ gas giving us 2 NOCl gas are given below. Here we have experiments 1-2 and 3 and each experiment has attached to it reacting concentrations and an initial rate. Now here it says determine the new rate if given new initial concentrations for NO and Cl₂. Now remember our sequence for solving is we first have to determine our reaction orders. Once we do that, then we can figure out our rate constant K, and then finally we can determine our new rate.

All right. So for step one, we're going to choose a reactant and look at two experiments where its concentration changes, but the other reactants stay the same. These other reactants we're going to ignore. So you're going to ignore the reactants whose concentrations remain the same. Here, we're going to look for the reaction order of NO. So let's make it X, Cl₂ would have Y. You can make the many variables you want, A, B, C, whatever. Here I just do X & Y. We have to look for two experiments where NO is changing but Cl₂ is staying the same. That occurs with experiments 2 and 3. With experiments 2 and 3, we see NO is changing and the concentrations of Cl₂ remain the same.

Once we've figured that out, we go to Step 2 where we create a pair of ratios for the reactant that sets rates equal to concentrations of the reactants. This is important. You place the larger rate value on top of the smaller rate value to get whole numbers when solving. And here you're going to raise the reactant concentrations to an unknown power or variable for the reaction order in salt. Alright, so if we take a look here, experiments 2 and 3, we can see that rate 3, its rate initial rate 3. Because it's connected to experiment 3, it's larger than initial rate 2. So that would mean that we're going to have rate 3 over rate 2 equals the concentrations of NO to the X. Now we're going to plug in the number so

18.2 9.08 = 0.0500 0.0250 ( 2 ) X

18.2 / 9.08 is approximately 2 and then 0.0500 / 0.0250 is 2 and it's still 2^X. Now you say 2 to what number gives you 2? The answer would be 1. So the reaction order for NO is 1.

Now we're going to do the same thing for step three. We're going to repeat the process for any remaining reactants until all reaction orders are determined, right? So now we have to look for Cl₂. We look for two experiments where Cl₂ is changing, but NO is staying the same. We see that happen with experiments 1 and 2. Now here initial rate 1 is larger than initial rate 2. So if we come down here, we're going to say rate 1 over rate 2 equals Cl₂ divided by Cl₂ to the Y. So let's see. That was 18.2 / 9.08. And then here we're going to plug in the concentrations for Cl₂. So here for Cl₂ it's 0.0510 and this is 0.0255 to the Y. This also comes out to 2 = 2^Y, 2 to one number gives us 2. The answer is 1. So it's first order for both of our reactants.

Now Step 4, if necessary. Here it is necessary because we need to find our new rate, and to find our new rate we have to figure out our rate constant. So here we're going to say, if necessary to solve for the rate constant K, plug in the reactant concentration and react in orders into the rate law. All right. So here we're going to say that our rate, we're going to say rate 1. You can use any of the rates, but just to keep it simple, always go with rate 1. So rate 1 equals K and we're going to say here NO to the one, Cl₂ to the one, OK. And then we're going to start plugging the numbers. So 18.2, we're looking for K. We don't know what K is. Come back up here. Let's use a concentration for. So since we're using rate 1, we have to use the concentrations of experiment 1. So that's 0.0250 and 0.0510 to the one and 0.0510 to the one. Alright, so here when we multiply these together, that's going to give me 0.001275 still multiplying with K. Rate 1 again is 18.2. Divide both sides by 0.001275 and we'll have our K. Here K equals 14117.647.

Now here we could technically give the units for K because remember to find the units of K it's M to the negative N + 1 times time inverse. And here's our overall order, which is 2, and it comes from adding your reaction orders together, so that's -2 + 1. Here. Let's just use seconds inverse, since our initial rates are molarities per second, so that would be M to the -1 times seconds inverse. OK, finally, we can figure out our new rate and again if necessary, we're going to say to solve for the new rate, plug in the K, the reaction orders and the additional reaction concentrations given. So here we're going to say that our new rate equals K and we're going to plug in the new concentrations given to us in the very beginning. So let's come up here. So here we have 0.0730 for our NO and then we have 0.0510 for our Cl₂. So those are the new concentrations we're going to plug into here. So let's come down here. So this is 0.0730 actually and that's again for NO to the one and Cl₂ to the one. So new rate. So K we got is 14117.647, NO is 0.0730 to the one, Cl₂ is 0.0510 to the one. When we plug all that in, that gives us 52.6 molarities per second for our new rate.

So we can see that if they're asking us for the new rate it is quite an ordeal. You have to go through a lot of things to get to your final answer. Remember, the sequence we're solving is important. First, figure out reaction orders before you can figure out your rate constant K before you can figure out your final new rate.

Given the following chemical reaction, A → B. If the concentration of A is doubled the rate increases by a factor of 2.83, what is the order of the reaction with respect to A.

• A. 1
• B. 0.5
• C. 1.5
• D. 0
• E. 2

In the experiments on the reaction 2 ICl (g) + H₂ (g) → I₂ (g) + 2 HCl (g), the following initial rate data were obtained. What is the overall order of the reaction?

• A. Third
• B. Second
• C. Zeroth
• D. Fourth
• E. First

The data below were collected for the following reaction:CH₃Cl (g) + 3 Cl₂ (g) → CCl₄ (g) + 3 HCl (g)

Calculate the value and units for the rate constant k.

• A. 1.25 M^-0.5s^-1
• B. 5.6 M^–1•s^–1
• C. 25 M^–3/2•s^–1
• D. 7.9 M^–5/2•s^–1

Here’s what students ask on this topic:

How can I find $k$ in the rate law?

To find the rate constant $k$ in the rate law, you need to know the form of the rate law and have some experimental data. The rate law expresses the rate of a chemical reaction as a function of the concentration of its reactants. It typically has the form:

Rate = $k{A}^m{B}^n$, where $A^m$ and $B^n$ are the concentrations of the reactants, and $m$ and $n$ are the orders of the reaction with respect to each reactant.

1. Determine the order of the reaction with respect to each reactant. This can be done by analyzing concentration and rate data from experiments.
2. Once you have the orders, write the rate law with the known orders.
3. Use experimental data that provides you with the concentrations of the reactants and the corresponding reaction rate.
4. Plug these values into the rate law equation.
5. Solve for $k$ by isolating it on one side of the equation.

Remember that $k$ should be consistent for a given reaction at a constant temperature, so if you have multiple sets of data, you can average the values of $k$ to get a more accurate result.

What is the overall reaction order for the following rate law: rate = $k\left[a\right]\left[b\right]\left[c\right]{]}^2$?

The overall reaction order of a rate law is determined by summing the exponents of the concentration terms in the rate equation. In the rate law you've provided, rate = $k\left[a\right]\left[b\right]\left[c\right]{]}^2$, you have three reactants: a, b, and c. Their respective concentration terms are raised to the power of 1 for a and b, and 2 for c.

To find the overall reaction order, you add up these exponents: 1 (for [a]) + 1 (for [b]) + 2 (for [c]²). When you sum these values, you get an overall reaction order of 4. This means the rate of the reaction is dependent on the concentration of the reactants to the fourth power; specifically, first-order with respect to reactants a and b, and second-order with respect to reactant c.

How can I find $k$ in the rate law?

To find the rate constant $k$ in the rate law, you need to know the form of the rate law and have some experimental data. The rate law expresses the rate of a chemical reaction as a function of the concentration of its reactants. It typically has the form:

Rate = $k{A}^m{B}^n$, where $A^m$ and $B^n$ are the concentrations of the reactants, and $m$ and $n$ are the orders of the reaction with respect to each reactant.

1. Determine the order of the reaction with respect to each reactant. This can be done by analyzing concentration and rate data from experiments.
2. Once you have the orders, write the rate law with the known orders.
3. Use experimental data that provides you with the concentrations of the reactants and the corresponding reaction rate.
4. Plug these values into the rate law equation.
5. Solve for $k$ by isolating it on one side of the equation.

Remember that $k$ should be consistent for a given reaction at a constant temperature, so if you have multiple sets of data, you can average the values of $k$ to get a more accurate result.

Given the rate law and table below, what are the values of m and n?

To determine the values of m and n in a rate law, you need to analyze how changes in the concentrations of reactants affect the rate of the reaction. The rate law is typically expressed as:

$\text{Rate =}k{\left[A\right]}^m{\left[B\right]}^n$

where [A] and [B] are the concentrations of reactants, and m and n are the orders of the reaction with respect to A and B, respectively.

To find the value of m, you would look at two experiments where the concentration of B is constant and the concentration of A changes. By comparing the change in rate with the change in concentration of A, you can determine m.

Similarly, to find the value of n, you would compare two experiments where the concentration of A is constant and the concentration of B changes. The change in rate with respect to the change in concentration of B will give you the value of n.

For example, if doubling the concentration of A while keeping B constant leads to a doubling of the rate, then m is 1 because the rate is directly proportional to [A]. If doubling [B] while keeping [A] constant quadruples the rate, then n is 2 because the rate is proportional to the square of [B].

Without the actual table of data, I can't provide specific values for m and n, but this is the method you would use to determine.