Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
3. Unit Circle
Trigonometric Functions on the Unit Circle
Problem 36
Textbook Question
Find one solution for each equation. Assume all angles involved are acute angles. See Example 3. cot(5θ + 2°) = tan(2θ + 4°)
 Verified step by step guidance
Verified step by step guidance1
Recognize that \( \cot(\alpha) = \tan(90^\circ - \alpha) \). Therefore, set \( 5\theta + 2^\circ = 90^\circ - (2\theta + 4^\circ) \).
Simplify the equation: \( 5\theta + 2^\circ = 90^\circ - 2\theta - 4^\circ \).
Combine like terms: \( 5\theta + 2^\circ + 2\theta + 4^\circ = 90^\circ \).
Simplify further: \( 7\theta + 6^\circ = 90^\circ \).
Solve for \( \theta \) by isolating it: \( 7\theta = 90^\circ - 6^\circ \).
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
0m:0sPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
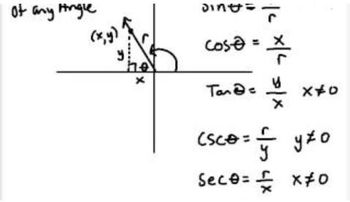
Cotangent and Tangent Functions
The cotangent function, cot(θ), is the reciprocal of the tangent function, tan(θ). This means that cot(θ) = 1/tan(θ). Understanding the relationship between these two functions is crucial for solving equations involving them, as it allows for the transformation of one function into another, facilitating the simplification of trigonometric equations.
Recommended video:

Introduction to Cotangent Graph
Angle Addition Formulas
Angle addition formulas are essential for simplifying expressions involving sums of angles. For example, the tangent of a sum can be expressed as tan(A + B) = (tan A + tan B) / (1 - tan A tan B). In this problem, recognizing how to apply these formulas to the angles in the cotangent and tangent functions will help in finding solutions for the given equation.
Recommended video:

Quadratic Formula
Acute Angles in Trigonometry
Acute angles are angles that measure less than 90 degrees. In trigonometry, the values of sine, cosine, tangent, cotangent, and other functions are positive for acute angles. This property is important when solving trigonometric equations, as it restricts the possible solutions to those that fall within the first quadrant, ensuring that the angles involved remain acute.
Recommended video:

Drawing Angles in Standard Position

 6:34m
6:34mWatch next
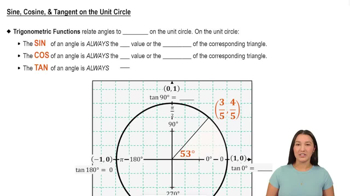
Master Sine, Cosine, & Tangent on the Unit Circle with a bite sized video explanation from Callie Rethman
Start learning