How many unique combinations of the quantum numbers l and ml are there when (b) n = 5?

Key Concepts

Quantum Numbers

Quantum numbers are sets of numerical values that describe the unique quantum state of an electron in an atom. There are four quantum numbers: principal (n), azimuthal (l), magnetic (ml), and spin (ms). Each quantum number provides specific information about the electron's energy level, shape of the orbital, orientation, and spin direction.

Principal Quantum Number (n)

The principal quantum number (n) indicates the main energy level or shell of an electron in an atom. It can take positive integer values (1, 2, 3, ...), with higher values corresponding to higher energy levels and greater distances from the nucleus. In this case, n = 5 means we are considering the fifth energy level.

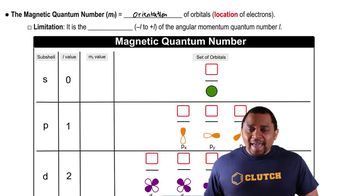
Azimuthal Quantum Number (l) and Magnetic Quantum Number (ml)

The azimuthal quantum number (l) defines the shape of the orbital and can take values from 0 to n-1. For n = 5, l can be 0, 1, 2, 3, or 4, corresponding to s, p, d, f, and g orbitals, respectively. The magnetic quantum number (ml) specifies the orientation of the orbital and can take values from -l to +l, resulting in multiple ml values for each l, thus creating unique combinations.