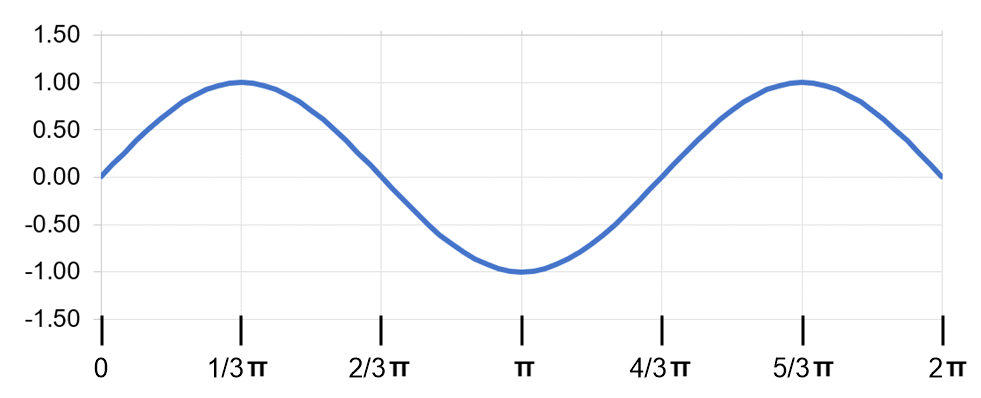
Consider a fictitious one-dimensional system with one electron. The wave function for the electron, drawn below, is c1x2 = sin x from x = 0 to x = 2p. (b) At what value or values of x will there be the greatest probability of finding the electron?

Key Concepts

Wave Function

The wave function is a mathematical description of the quantum state of a system, representing the probability amplitude of finding a particle in a given position. In this case, the wave function is given as sin(x), which describes the behavior of the electron in a one-dimensional system. The square of the wave function's magnitude gives the probability density, indicating where the electron is likely to be found.

Probability Density

Probability density is derived from the wave function and indicates the likelihood of finding a particle in a specific region of space. For a wave function ψ(x), the probability density is given by |ψ(x)|². In the context of the provided wave function sin(x), the peaks of the graph correspond to higher probabilities of locating the electron, while the nodes (where the function crosses zero) indicate positions where the electron cannot be found.

Nodes and Antinodes

In wave mechanics, nodes are points where the wave function is zero, resulting in zero probability of finding the particle, while antinodes are points where the wave function reaches its maximum value, indicating the highest probability of finding the particle. In the graph of sin(x), the peaks represent antinodes, where the electron is most likely to be found, while the points where the function crosses the x-axis are nodes, indicating locations of zero probability.