Imagine the primitive cubic lattice. Now imagine grabbing the top of it and stretching it straight up. All angles remain 90. What kind of primitive lattice have you made?
The unit cell of nickel arsenide is shown here. (b) What is the empirical formula?
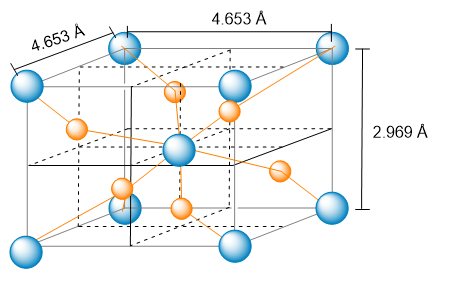

Verified Solution
Key Concepts
Unit Cell

Empirical Formula

Coordination Number

Which of the three-dimensional primitive lattices has a unit cell where none of the internal angles is 90? (a) Orthorhombic, (b) hexagonal, (c) rhombohedral, (d) triclinic, (e) both rhombohedral and triclinic.
What is the minimum number of atoms that could be contained in the unit cell of an element with a face-centered cubic lattice? (a) 1, (b) 2, (c) 3, (d) 4, (e) 5.
The unit cell of a compound containing potassium, aluminum, and fluorine is shown here. (a) What type of lattice does this crystal possess (all three lattice vectors are mutually perpendicular)?
Consider the unit cells shown here for three different structures that are commonly observed for metallic elements. (a) Which structure(s) corresponds to the densest packing of atoms?
Consider the unit cells shown here for three different structures that are commonly observed for metallic elements. (b) Which structure(s) corresponds to the least dense packing of atoms?
