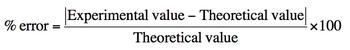Understanding experimental error is crucial in scientific measurements, as it directly relates to the concepts of accuracy and precision. Experimental error can be categorized into two main types: random errors and systematic errors. Random errors arise from unpredictable fluctuations in measurements, leading to results that can be either too high or too low. This lack of precision means that if multiple measurements are taken, they may vary significantly. To mitigate random errors, it is advisable to take several measurements and calculate their average, which helps to smooth out these fluctuations.
On the other hand, systematic errors are consistent and predictable, resulting in measurements that are consistently too high or too low, but not both. For instance, if a scale consistently reads 1 gram too heavy, every measurement taken will reflect this bias. Systematic errors can be more challenging to identify because they may not show variability; repeated measurements may yield the same erroneous value, leading one to mistakenly believe they are accurate.
To quantify the accuracy of measurements, the concept of percent error is employed. The formula for percent error is given by:
\[\text{Percent Error} = \left( \frac{|\text{Experimental Value} - \text{Theoretical Value}|}{\text{Theoretical Value}} \right) \times 100\]
In this formula, the experimental value is the result obtained from measurements, while the theoretical value is the expected or accepted value from literature. A percent error of less than 10% is generally considered acceptable in most experiments, indicating that the measurements are reasonably precise.
For example, if a theoretical value is 25 grams and the experimental value obtained is 24.8 grams, the percent error can be calculated to assess the precision of the measurement. A small percent error suggests that the experimental results are close to the theoretical expectations, reinforcing the reliability of the measurements taken.
In summary, distinguishing between random and systematic errors is essential for improving measurement accuracy and precision. By understanding these concepts and applying the percent error formula, students can better evaluate their experimental results and enhance their scientific inquiry skills.