Ch. 2 - Graphs and Functions
 Back
Back- Without using paper and pencil, evaluate each expression given the following functions. ƒ(x)=x+1 and g(x)=x^2 (ƒ+g)(2)
Problem 1
- Without using paper and pencil, evaluate each expression given the following functions. ƒ(x)=x+1 and g(x)=x^2 (ƒ-g)(2)
Problem 2
- Without using paper and pencil, evaluate each expression given the following functions. ƒ(x)=x+1 and g(x)=x^2 (ƒg)(2)
Problem 3
- Without using paper and pencil, evaluate each expression given the following functions. ƒ(x)=x+1 and g(x)=x^2 (ƒ/g)(2)
Problem 4
- Without using paper and pencil, evaluate each expression given the following functions. ƒ(x)=x+1 and g(x)=x^2 (ƒ∘g)(2)
Problem 5
- Without using paper and pencil, evaluate each expression given the following functions. ƒ(x)=x+1 and g(x)=x^2 (g∘ƒ)(2)
Problem 6
- Fill in the blank(s) to correctly complete each sentence. The function g(x)=√x has domain ________.
Problem 7
Problem 9
Without actually graphing, identify the type of graph that each equation has.
- Let ƒ(x)=x^2+3 and g(x)=-2x+6. Find each of the following. See Example 1. (ƒ+g)(3)
Problem 11
- Write an equation for each line described. Give answers in standard form for Exercises 11–20 and in slope-intercept form (if possible) for Exercises 21–32. through (1,3), m = -2
Problem 11
- Let ƒ(x)=x^2+3 and g(x)=-2x+6. Find each of the following. See Example 1. (ƒ+g)(-5)
Problem 12
- Determine the intervals of the domain over which each function is continuous. See Example 1.
Problem 13
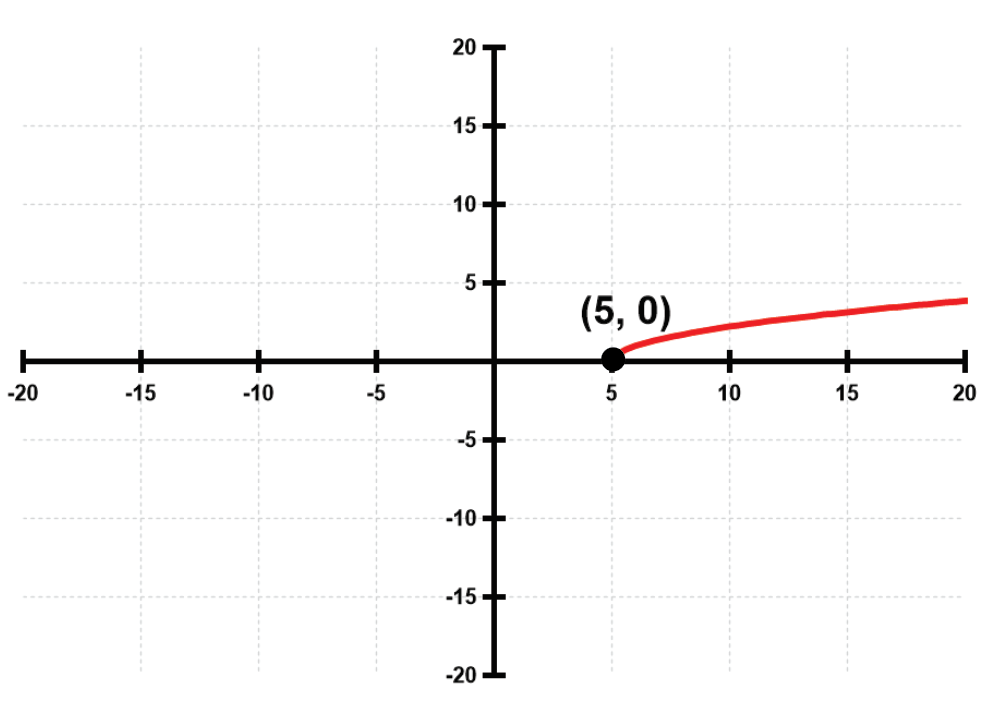
- Let ƒ(x)=x^2+3 and g(x)=-2x+6. Find each of the following. See Example 1. (ƒ-g)(-1)
Problem 13
- Write an equation for each line described. Give answers in standard form for Exercises 11–20 and in slope-intercept form (if possible) for Exercises 21–32. through (-5,4), m = -3/2
Problem 13
- Let ƒ(x)=x^2+3 and g(x)=-2x+6. Find each of the following. See Example 1. (ƒ-g)(4)
Problem 14
- Write an equation for each line described. Give answers in standard form for Exercises 11–20 and in slope-intercept form (if possible) for Exercises 21–32. through (-8,4), undefined slope
Problem 15
Problem 15
Let ƒ(x)=x^2+3 and g(x)=-2x+6. Find each of the following. See Example 1. (ƒg)(4)
- Let ƒ(x)=x^2+3 and g(x)=-2x+6. Find each of the following. See Example 1. (ƒg)(-3)
Problem 16
- Graph each function. See Examples 1 and 2. ƒ(x)=3|x|
Problem 17
- Let ƒ(x)=x^2+3 and g(x)=-2x+6. Find each of the following. See Example 1. (ƒ/g)(-1)
Problem 17
- Let ƒ(x)=x^2+3 and g(x)=-2x+6. Find each of the following. See Example 1. (ƒ/g)(5)
Problem 18
- Graph each function. See Examples 1 and 2. ƒ(x)=2/3|x|
Problem 19
- For the pair of functions defined, find (ƒ+g)(x).Give the domain of each. See Example 2. ƒ(x)=3x+4, g(x)=2x-5
Problem 19
- For the pair of functions defined, find (ƒ-g)(x).Give the domain of each. See Example 2. ƒ(x)=3x+4, g(x)=2x-6
Problem 19
- For the pair of functions defined, find (ƒg)(x).Give the domain of each. See Example 2. ƒ(x)=3x+4, g(x)=2x-7
Problem 19
- For the pair of functions defined, find (f/g)(x).Give the domain of each. See Example 2. ƒ(x)=3x+4, g(x)=2x-8
Problem 19
- Write an equation for each line described. Give answers in standard form for Exercises 11–20 and in slope-intercept form (if possible) for Exercises 21–32. through (-1,3), and (3,4)
Problem 19
- For the pair of functions defined, find (ƒ+g)(x).Give the domain of each. See Example 2. ƒ(x)=2x^2-3x, g(x)=x^2-x+3
Problem 21
- For the pair of functions defined, find (ƒ-g)(x). Give the domain of each. See Example 2. ƒ(x)=2x^2-3x, g(x)=x^2-x+3
Problem 21
- For the pair of functions defined, find (ƒg)(x). Give the domain of each. See Example 2. ƒ(x)=2x^2-3x, g(x)=x^2-x+3
Problem 21

