Write an equation for each line described. Give answers in standard form for Exercises 11–20 and in slope-intercept form (if possible) for Exercises 21–32. through (-8,4), undefined slope

Key Concepts

Undefined Slope

An undefined slope occurs in a vertical line, where the change in the y-coordinates is non-zero while the change in the x-coordinates is zero. This means that the line does not rise or fall as it moves horizontally, resulting in a slope that cannot be calculated. The equation of a vertical line can be expressed in the form x = a, where 'a' is the x-coordinate of any point on the line.

Standard Form of a Line

The standard form of a linear equation is typically written as Ax + By = C, where A, B, and C are integers, and A should be non-negative. This form is useful for quickly identifying the x- and y-intercepts of the line. To convert an equation into standard form, one can rearrange the terms to isolate the constants on one side of the equation.

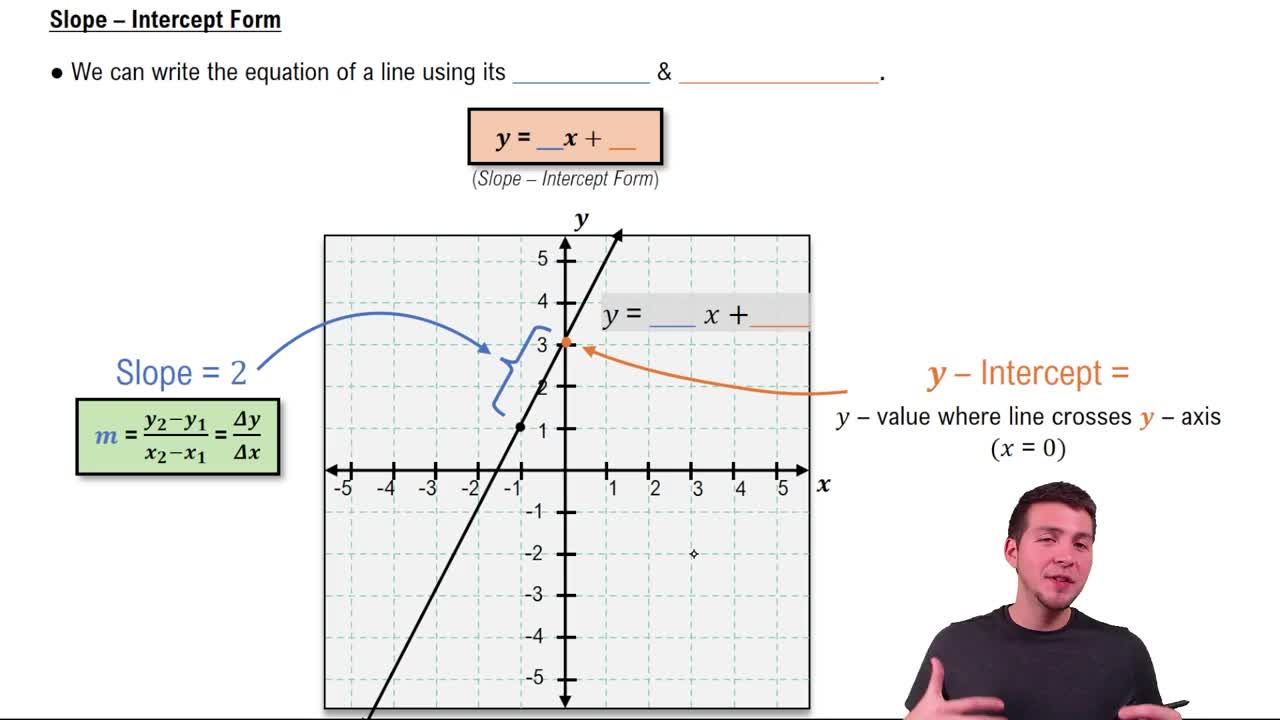
Slope-Intercept Form

The slope-intercept form of a linear equation is given by y = mx + b, where m represents the slope of the line and b is the y-intercept. This form is particularly useful for graphing because it directly provides the slope and the point where the line crosses the y-axis. To convert from standard form to slope-intercept form, one can solve for y in terms of x.