Here are the essential concepts you must grasp in order to answer the question correctly.
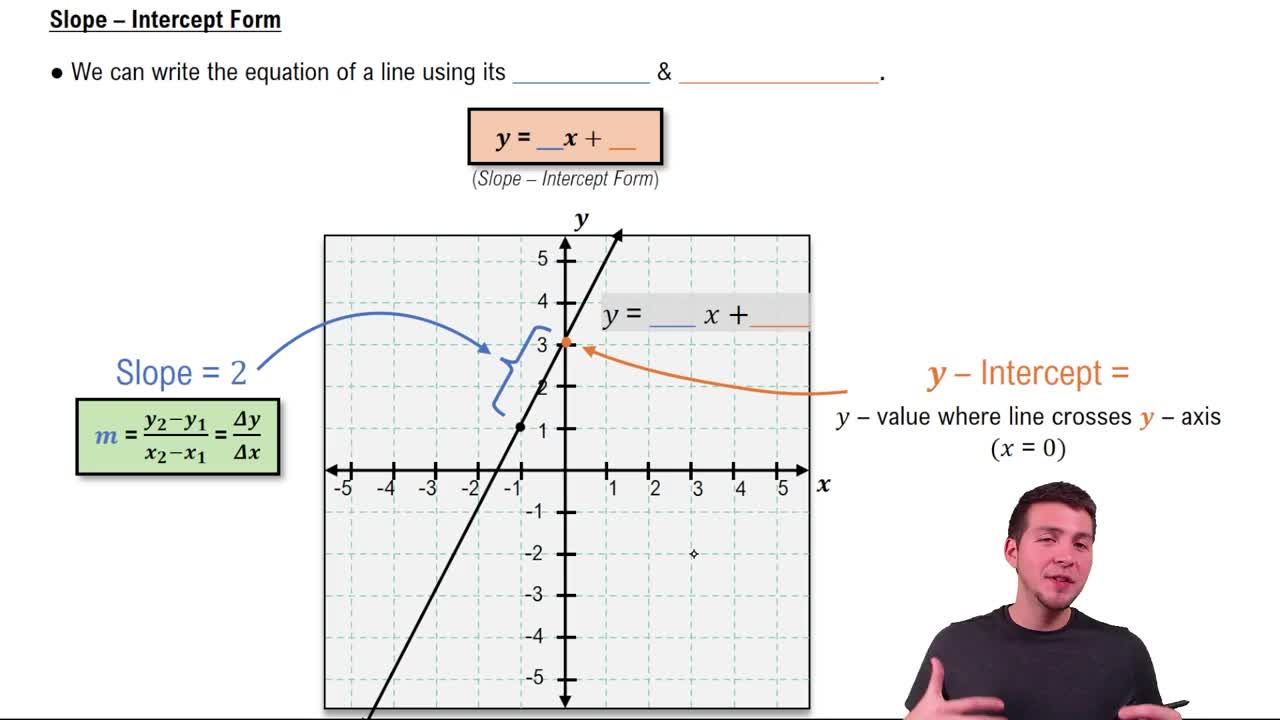
Slope-Intercept Form
The slope-intercept form of a linear equation is expressed as y = mx + b, where m represents the slope of the line and b is the y-intercept. This form is useful for quickly identifying the slope and where the line crosses the y-axis. To convert a standard form equation to slope-intercept form, you can solve for y.
Recommended video:
Standard Form of a Linear Equation
The standard form of a linear equation is typically written as Ax + By = C, where A, B, and C are integers, and A should be non-negative. This form is useful for easily identifying intercepts and is often used in systems of equations. To convert to slope-intercept form, you can rearrange the equation to isolate y.
Recommended video:
Standard Form of Line Equations
Finding the Slope Between Two Points
The slope of a line between two points (x1, y1) and (x2, y2) is calculated using the formula m = (y2 - y1) / (x2 - x1). This value indicates the steepness and direction of the line. In the context of the given points (-1, 3) and (3, 4), calculating the slope is the first step in writing the equation of the line that passes through these points.
Recommended video: