Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
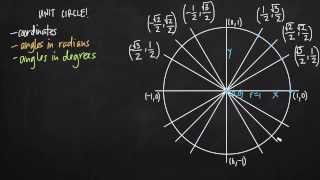
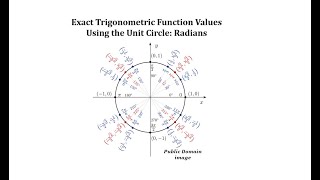
3. Unit Circle
Defining the Unit Circle
Problem 3.41b
Textbook Question
Find a calculator approximation to four decimal places for each circular function value. See Example 3.
sec 2.8440
 Verified step by step guidance
Verified step by step guidance1
Understand that secant (sec) is the reciprocal of cosine, so \( \sec \theta = \frac{1}{\cos \theta} \).
Identify the angle given in the problem, which is \( \theta = 2.8440 \) radians.
Use a calculator to find \( \cos(2.8440) \).
Calculate the reciprocal of the cosine value obtained: \( \sec(2.8440) = \frac{1}{\cos(2.8440)} \).
Round the result to four decimal places to get the final approximation.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
0m:0sPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Circular Functions
Circular functions, also known as trigonometric functions, relate the angles of a circle to the ratios of its sides. The primary circular functions include sine, cosine, tangent, and their reciprocals: cosecant, secant, and cotangent. Understanding these functions is essential for evaluating angles and their corresponding values in various contexts, such as in the given problem.
Recommended video:
Graphs of Common Functions
Secant Function
The secant function is defined as the reciprocal of the cosine function. Mathematically, sec(θ) = 1/cos(θ). It is important to know how to compute the secant of an angle, especially when using a calculator, as it directly relates to the cosine value of that angle. In this case, finding sec(2.8440) requires calculating the cosine first.
Recommended video:

Graphs of Secant and Cosecant Functions
Calculator Approximations
Calculator approximations involve using a scientific calculator to find numerical values of trigonometric functions to a specified degree of accuracy, such as four decimal places. This process typically includes entering the angle in radians or degrees and selecting the appropriate function. Understanding how to read and interpret these approximations is crucial for solving problems that require precise values.
Recommended video:

How to Use a Calculator for Trig Functions

 6:11m
6:11mWatch next
Master Introduction to the Unit Circle with a bite sized video explanation from Callie Rethman
Start learningRelated Videos
Related Practice