Here are the essential concepts you must grasp in order to answer the question correctly.
Ohm's Law
Ohm's Law states that the current (I) flowing through a conductor between two points is directly proportional to the voltage (V) across the two points and inversely proportional to the resistance (R) of the conductor. This relationship is expressed mathematically as I = V/R. Understanding this law is crucial for analyzing circuits, as it allows us to calculate the current based on the voltage supplied and the total resistance in the circuit.
Recommended video:
Series and Parallel Resistor Configurations
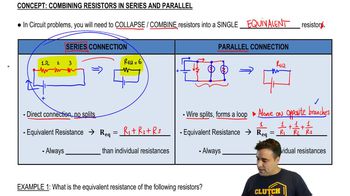
Resistors can be arranged in series or parallel configurations, affecting the total resistance in a circuit. In a series configuration, the total resistance is the sum of individual resistances (R_total = R1 + R2 + ...). In a parallel configuration, the total resistance can be calculated using the formula 1/R_total = 1/R1 + 1/R2 + ... This distinction is essential for determining how the resistors in the triangular array will influence the overall current drawn from the battery.
Recommended video:
Combining Resistors in Series & Parallel
Equivalent Resistance
The equivalent resistance of a circuit is a single resistance that can replace a combination of resistors while maintaining the same current and voltage characteristics. For the triangular array of resistors, calculating the equivalent resistance is necessary to simplify the circuit analysis. This allows us to apply Ohm's Law effectively to find the current drawn from the battery when connected across specific points in the circuit.
Recommended video:
Find Equivalent Capacitance #1

 Verified step by step guidance
Verified step by step guidance