Here are the essential concepts you must grasp in order to answer the question correctly.
Density of Gold
Density is a measure of mass per unit volume, and for gold, it is approximately 19.32 g/cm³. This property is crucial for determining the volume of the gold cube based on its mass. By knowing the density, we can calculate how much space the gold occupies, which is essential for finding the dimensions of the cube.
Recommended video:
Volume of a Cube
The volume of a cube is calculated using the formula V = a³, where 'a' is the length of one side of the cube. To find the height of the cube, we need to determine the total volume of gold represented by the million-dollar value and then extract the cube root of that volume to find the height.
Recommended video:
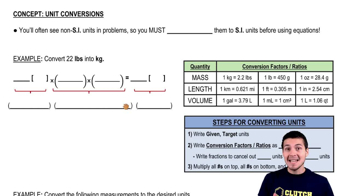
Conversion of Units
In this problem, converting between different units is essential, particularly from troy ounces to grams and then to cubic centimeters. Understanding how to perform these conversions accurately ensures that all measurements are consistent, allowing for correct calculations of mass, volume, and ultimately the dimensions of the gold cube.
Recommended video: