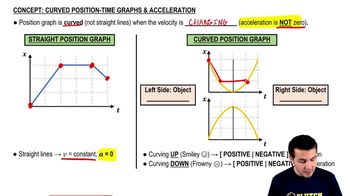
Textbook Question
A physics professor leaves her house and walks along the sidewalk toward campus. After 5 min it starts to rain, and she returns home. Her distance from her house as a function of time is shown in Fig. E2.10. At which of the labeled points is her velocity (a) zero?
544
views