Here are the essential concepts you must grasp in order to answer the question correctly.
Thermal Efficiency
Thermal efficiency is a measure of how well a heat engine converts heat from a hot reservoir into work. It is defined as the ratio of the work output to the heat input from the hot reservoir, typically expressed as a percentage. The formula for thermal efficiency (η) is η = W/Qh, where W is the work done by the engine and Qh is the heat absorbed from the hot reservoir.
Recommended video:
Thermal Efficiency & The Second Law of Thermodynamics
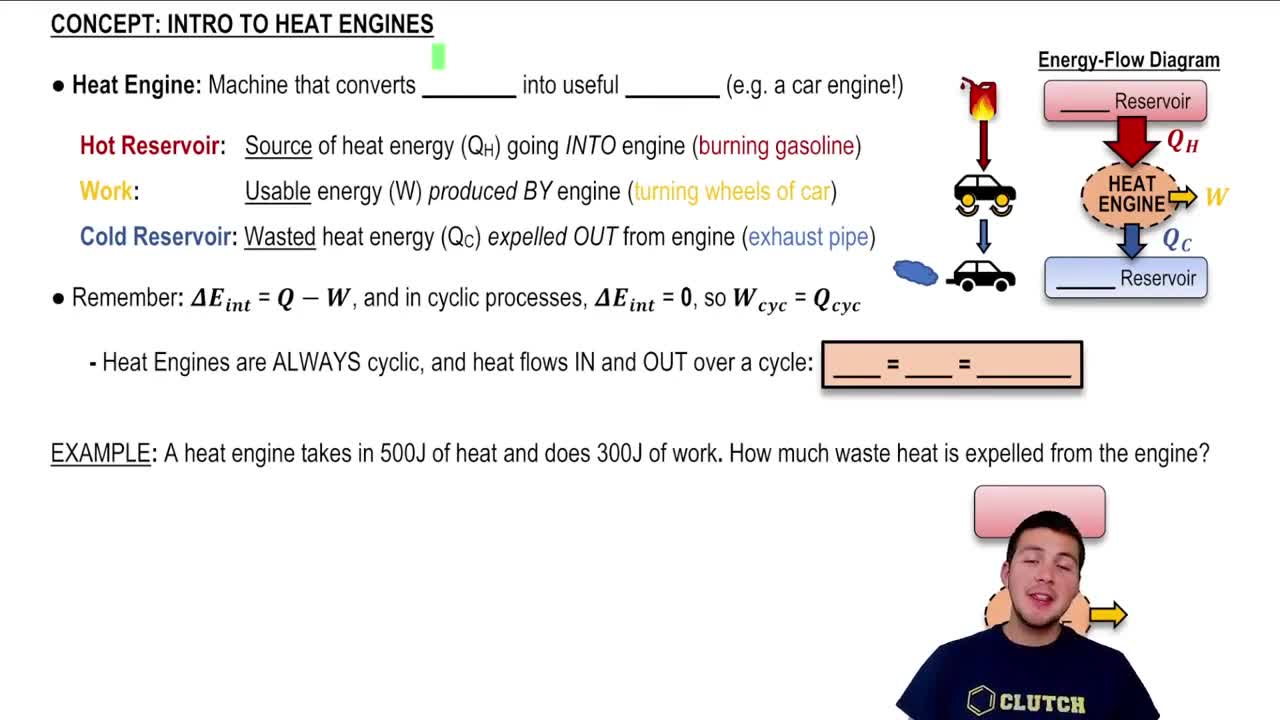
Heat Reservoirs
In thermodynamics, a heat reservoir is a large body that can supply or absorb heat without undergoing a significant change in temperature. In the context of a heat engine, there are typically two reservoirs: a hot reservoir that provides heat to the engine and a cold reservoir that absorbs waste heat. Understanding the role of these reservoirs is crucial for analyzing the performance and efficiency of the engine.
Recommended video:
Introduction to Heat Engines
First Law of Thermodynamics
The First Law of Thermodynamics, also known as the law of energy conservation, states that energy cannot be created or destroyed, only transformed from one form to another. For a heat engine, this principle implies that the heat energy supplied from the hot reservoir (Qh) is equal to the work done by the engine (W) plus the heat rejected to the cold reservoir (Qc). This relationship is essential for calculating both thermal efficiency and the heat extracted from the hot reservoir.
Recommended video:
The First Law of Thermodynamics