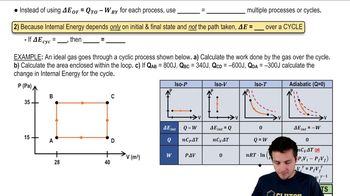
Here are the essential concepts you must grasp in order to answer the question correctly.
First Law of Thermodynamics
The First Law of Thermodynamics states that energy cannot be created or destroyed, only transformed from one form to another. In the context of a heat engine, this principle relates the change in internal energy (∆Eₜₕ) to the work done by the system (Wₛ) and the heat exchanged (Q) with the surroundings, expressed as ∆Eₜₕ = Q - Wₛ.
Recommended video:
The First Law of Thermodynamics
Monatomic Gas Properties
Monatomic gases, such as helium or argon, consist of single atoms and exhibit specific thermodynamic behaviors. Their internal energy is directly proportional to temperature and can be calculated using the formula U = (3/2)nRT, where n is the number of moles, R is the ideal gas constant, and T is the temperature in Kelvin. Understanding these properties is essential for analyzing the energy changes in the heat engine.
Recommended video:
Properties of Cyclic Thermodynamic Processes
Thermodynamic Processes
Thermodynamic processes describe the changes in state variables of a system, such as pressure, volume, and temperature, during energy transfer. Common processes include isothermal (constant temperature), adiabatic (no heat exchange), and isochoric (constant volume). Each process affects the heat engine's performance and efficiency, influencing the values of ∆Eₜₕ, Wₛ, and Q in the table required for the question.
Recommended video:
Properties of Cyclic Thermodynamic Processes