Here are the essential concepts you must grasp in order to answer the question correctly.
Ideal Gas Law
The Ideal Gas Law relates the pressure, volume, temperature, and number of moles of an ideal gas through the equation PV = nRT. This law is fundamental in understanding how gases behave under various conditions and is essential for solving problems involving gas equations.
Recommended video:
Ideal Gases and the Ideal Gas Law
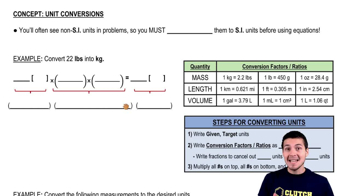
Pressure Units
Pressure is a measure of force applied per unit area, commonly expressed in units such as pascals (Pa), kilopascals (kPa), or atmospheres (atm). Understanding how to convert between these units is crucial for accurately interpreting and solving problems involving gas pressure.
Recommended video:
Pressure and Atmospheric Pressure
Temperature Conversion
Temperature in physics is often measured in Kelvin (K), Celsius (°C), or Fahrenheit (°F). The conversion between these scales is vital, especially in thermodynamic equations, where absolute temperature in Kelvin is required for calculations involving gas laws.
Recommended video:
 Verified step by step guidance
Verified step by step guidance