Here are the essential concepts you must grasp in order to answer the question correctly.
Ideal Gas Law
The Ideal Gas Law relates the pressure, volume, temperature, and number of moles of a gas through the equation PV = nRT. This law is fundamental in understanding the behavior of gases under various conditions. In this context, it can be used to calculate the temperature at different states of the gas as it undergoes changes in pressure and volume.
Recommended video:
Ideal Gases and the Ideal Gas Law
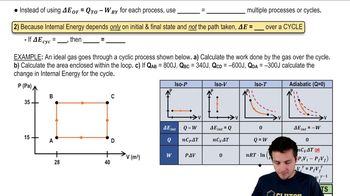
Thermodynamic Processes
Thermodynamic processes describe how a system changes from one state to another, often involving heat transfer and work done. The process shown in the figure likely involves isothermal, isobaric, or adiabatic changes, which affect how temperature and pressure relate to volume. Understanding these processes is crucial for analyzing the gas behavior between points A, B, and C.
Recommended video:
Properties of Cyclic Thermodynamic Processes
State Variables
State variables such as pressure (P), volume (V), and temperature (T) define the state of a gas at any given point. Each point in the graph represents a unique state of the gas, and knowing these variables allows for the application of the Ideal Gas Law and other thermodynamic principles. Identifying these variables at points A, B, and C is essential for solving the problem.
Recommended video:
Impulse with Variable Forces