Evaluate the cross products and A ✕ B and C ✕ D.

Key Concepts

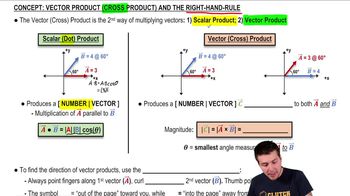
Cross Product

The cross product of two vectors results in a third vector that is perpendicular to the plane formed by the original vectors. It is calculated using the formula A × B = |A||B|sin(θ)n, where θ is the angle between the vectors and n is the unit vector perpendicular to the plane. The magnitude of the cross product represents the area of the parallelogram formed by the two vectors.

Vector Magnitude

The magnitude of a vector is a measure of its length and is calculated using the Pythagorean theorem for two-dimensional vectors. For a vector represented as A = (Ax, Ay), the magnitude is given by |A| = √(Ax² + Ay²). In the context of the question, the magnitudes of vectors E and F are 3 and 4, respectively, which are essential for calculating their cross product.

Angle Between Vectors

The angle between two vectors is crucial for determining the sine component in the cross product formula. In this case, the angle is given as 30°, which affects the magnitude of the resulting vector from the cross product. Understanding how to find and use this angle is key to solving problems involving vector operations.