Vector A ＝ 3î＋ĵ and vector B＝ 3î ─ 2ĵ ＋ 2k. What is the cross product A ✕ B?

Key Concepts

Vector Operations

Vector operations involve mathematical manipulations of vectors, including addition, subtraction, and multiplication. The cross product is a specific operation that takes two vectors and produces a third vector that is perpendicular to the plane formed by the original vectors. Understanding how to perform these operations is essential for solving problems involving vectors.

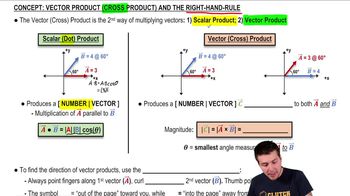
Cross Product

The cross product of two vectors A and B, denoted as A × B, results in a vector that is orthogonal to both A and B. The magnitude of the cross product is given by |A||B|sin(θ), where θ is the angle between the two vectors. The direction of the resulting vector is determined by the right-hand rule, which is crucial for visualizing the orientation of the cross product.

Coordinate System

In physics, vectors are often represented in a three-dimensional Cartesian coordinate system, defined by the unit vectors î, ĵ, and k. Each vector can be expressed in terms of its components along these axes. Understanding how to manipulate vectors in this coordinate system is vital for calculating operations like the cross product, as it allows for clear representation and computation of vector components.