14. Torque & Rotational Dynamics
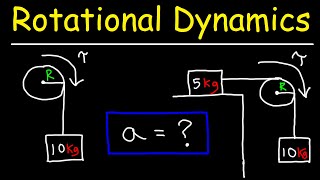
Torque & Acceleration (Rotational Dynamics)
Learn with other creators
Practice this topic
- Multiple Choice
Suppose that piano has a long, thin bar ran through it (totally random), shown below as the vertical red line, so that it is free to rotate about a vertical axis through the bar. You push the piano with a horizontal 100 N (blue arrow), causing it to spin about its vertical axis with 0.3 rad/s2 . Your force acts at a distance of 1.1 m from the bar, and is perpendicular to a line connecting it to the bar (green dotted line). What is the piano's moment of inertia about its vertical axis?
1501views14rank2comments - Multiple ChoiceA particle is moving in circular motion with a radius of . At one instant in time its speed was and it was slowing down at a rate of . What was the magnitude of the net force on the particle at this instant?1279views
- Multiple ChoiceA hollow sphere with a radius of 0.31 m is placed on an inclined plane that makes an angle with the floor. Assuming the sphere rolls without slipping, what will be the magnitude of the acceleration of the sphere down in the incline?1110views
- Textbook Question
A cord is wrapped around the rim of a solid uniform wheel 0.250 m in radius and of mass 9.20 kg. A steady horizontal pull of 40.0 N to the right is exerted on the cord, pulling it off tangentially from the wheel. The wheel is mounted on frictionless bearings on a horizontal axle through its center. Find the magnitude and direction of the force that the axle exerts on the wheel.
3702views2rank - Textbook Question
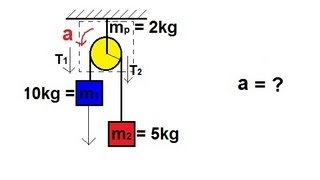
A 12.0-kg box resting on a horizontal, frictionless surface is attached to a 5.00-kg weight by a thin, light wire that passes over a frictionless pulley (Fig. E10.16). The pulley has the shape of a uniform solid disk of mass 2.00 kg and diameter 0.500 m. After the system is released, find the acceleration of the box.
6659views - Textbook Question
A 15.0-kg bucket of water is suspended by a very light rope wrapped around a solid uniform cylinder 0.300 m in diameter with mass 12.0 kg. The cylinder pivots on a frictionless axle through its center. The bucket is released from rest at the top of a well and falls 10.0 m to the water. With what speed does the bucket strike the water?
2412views - Textbook Question
A 2.00-kg textbook rests on a frictionless, horizontal surface. A cord attached to the book passes over a pulley whose diameter is 0.150 m, to a hanging book with mass 3.00 kg. The system is released from rest, and the books are observed to move 1.20 m in 0.800 s. What is the tension in each part of the cord?
2155views2rank - Multiple ChoiceThe maximum torque of a 100-turn loop of wire that has an area of 0.15 m² and is carrying 1.5 A of current in a uniform magnetic field of 2.0 T is:703views