25. Electric Potential
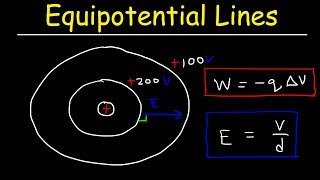
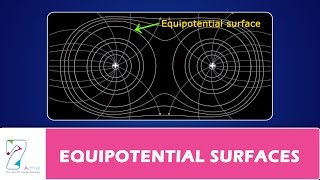
Equipotential Surfaces
Learn with other creators
Practice this topic
- Multiple Choice
Draw the electric field that corresponds to the equipotential surfaces shown in the following figure. Note that the potential is decreasing in the upward direction.
1423views21rank - Textbook Question
A very large plastic sheet carries a uniform charge density of nC/m2 on one face. As you move away from the sheet along a line perpendicular to it, does the potential increase or decrease? How do you know, without doing any calculations? Does your answer depend on where you choose the reference point for potential?
1762views - Textbook Question
Suppose the charge on the outer sphere is not but a negative charge of different magnitude, say . Show that the answers for parts (b) and (c) are the same as before but the answer for part (d) is different. Note: Part (a) asked to calculate the potential for (i) ; (ii) ; (iii) . (Hint: The net potential is the sum of the potentials due to the individual spheres.) Take to be zero when is infinite. Part (b) asked to show that the potential of the inner sphere with respect to the outer is . Part (c) asked to use and the result from part (a) to show that the electric field at any point between the spheres has magnitude . Part (d) asked to use and the result from part (a) to find the electric field at a point outside the larger sphere at a distance from the center, where .
1183views1rank - Textbook Question
A metal sphere with radius is supported on an insulating stand at the center of a hollow, metal, spherical shell with radius . There is charge on the inner sphere and charge on the outer spherical shell. Use and the result from part (a) to find the electric field at a point outside the larger sphere at a distance from the center, where . Note: Part (a) asked to calculate the potential for (i) ; (ii) ; (iii) . (Hint: The net potential is the sum of the potentials due to the individual spheres.) Take to be zero when is infinite..
2428views - Textbook Question
A metal sphere with radius is supported on an insulating stand at the center of a hollow, metal, spherical shell with radius . There is charge on the inner sphere and charge on the outer spherical shell. Use and the result from part (a) to show that the electric field at any point between the spheres has magnitude . Note: Part (a) asked to calculate the potential for (i) ; (ii) ; (iii) . (Hint: The net potential is the sum of the potentials due to the individual spheres.) Take to be zero when is infinite..
783views - Multiple Choice
Which of the following statements correctly describes an equipotential surface?
53views - Multiple Choice
If the surfaces in a region are spaced closer together in one area and farther apart in another, what does this indicate about the strength of the field in those regions?
52views - Multiple Choice
A surface will be an surface if which of the following conditions is satisfied?
49views