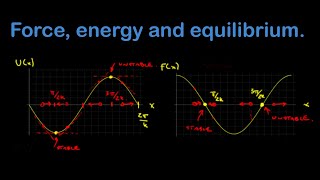
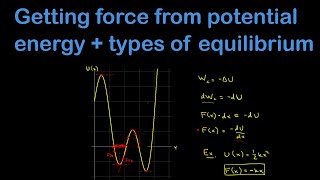
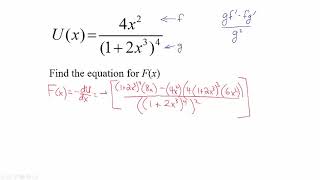10. Conservation of Energy
Force & Potential Energy
Learn with other creators
Practice this topic
- Multiple Choice
A particle with a mass of 0.1kg moves according to the Potential Energy graph shown. What minimum speed does the particle need at Point A to reach Point B?
2317views24rank1comments - Textbook Question
A system in which only one particle moves has the potential energy shown in FIGURE EX10.31. What is the x-component of the force on the particle at x = 5, 15, and 25 cm?
2036views - Textbook Question
In FIGURE EX10.28, what is the maximum speed a 200 g particle could have at x = 2.0 m and never reach x = 6.0 m?
1602views - Textbook Question
FIGURE EX10.28 shows the potential-energy diagram for a 500 g particle as it moves along the x-axis. Suppose the particle's mechanical energy is 12 J. Where are the particle's turning points?
1758views - Textbook Question
FIGURE EX10.25 is the potential-energy diagram for a 20 g particle that is released from rest at x = 1.0 m. What is the particle's maximum speed? At what position does it have this speed?
2211views