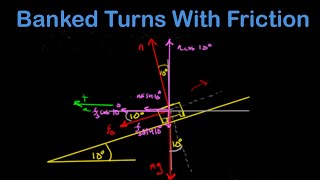
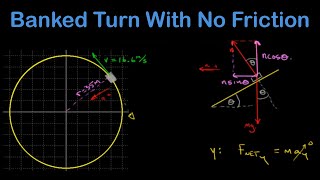
07:31Ideal banking angle car rounds a banked turn without friction, frictionless banked curveZak's Lab589views
Multiple ChoiceA bobsled turn banked at 78° is taken at 24 m/s. Assume it is ideally banked and there is no friction between the ice and the bobsled. Calculate the centripetal acceleration of the bobsled.822views14rank1comments
Textbook QuestionA 1125-kg car and a 2250-kg pickup truck approach a curve on a highway that has a radius of 225 m. (a) At what angle should the highway engineer bank this curve so that vehicles traveling at 65.0 mi/h can safely round it regardless of the condition of their tires? Should the heavy truck go slower than the lighter car?2270views
Textbook QuestionA car drives at a constant speed around a banked circular track with a diameter of 145 m. The motion of the car can be described in a coordinate system with its origin at the center of the circle. At a particular instant the car’s acceleration in the horizontal plane is given bya→ = (-15.7 î - 23.2 ĵ)m/s² .(a) What is the car’s speed?130views
Textbook Question(II) How large must the coefficient of static friction be between the tires and the road if a car is to round a level curve of radius 85 m at a speed of 95 km/h?133views
Textbook QuestionAn airplane feels a lift force L perpendicular to its wings. In level flight, the lift force points straight up and is equal in magnitude to the gravitational force on the plane. When an airplane turns, it banks by tilting its wings, as seen from behind, by an angle from horizontal. This causes the lift to have a radial component, similar to a car on a banked curve. If the lift had constant magnitude, the vertical component of L would now be smaller than the gravitational force, and the plane would lose altitude while turning. However, you can assume that the pilot uses small adjustments to the plane's control surfaces so that the vertical component of L continues to balance the gravitational force throughout the turn. a. Find an expression for the banking angle θ needed to turn in a circle of radius r while flying at constant speed v.717views
Textbook QuestionA banked curve of radius R in a new highway is designed so that a car traveling at speed v₀ can negotiate the turn safely on glare ice (zero friction). If a car travels too slowly, then it will slip toward the center of the circle. If it travels too fast, it will slip away from the center of the circle. If the coefficient of static friction increases, it becomes possible for a car to stay on the road while traveling at a speed within a range from vₘᵢₙ to vₘₐₓ . Derive formulas for vₘᵢₙ and vₘₐₓ as functions of μₛ, v₀ and R.381views
Textbook Question(II) A 1250-kg car rounds a curve of radius 68 m banked at an angle of 14°. If the car is traveling at 85 km/h, will a friction force be required? If so, how much and in what direction?210views
Textbook QuestionAn airplane traveling at 510 km/h needs to reverse its course. The pilot decides to accomplish this by banking the wings at an angle of 38° while moving in a level circular path.<IMAGE>(a) Find the time needed to reverse course.170views
Textbook QuestionA car drives at a constant speed around a banked circular track with a diameter of 145 m. The motion of the car can be described in a coordinate system with its origin at the center of the circle. At a particular instant the car’s acceleration in the horizontal plane is given bya→ = (-15.7 î - 23.2 ĵ)m/s² .(b) Where (x and y) is the car at this instant?269views
Textbook QuestionConsider a train that rounds a curve with a radius of 530 m at a speed of 160 km/h (approximately 100 mi/h ).(b) Calculate the friction force on the passenger if the train tilts at an angle of 8.0° toward the center of the curve.279views
08:19
