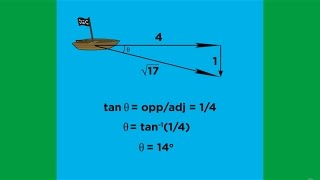
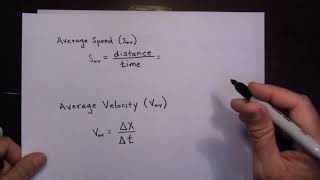2. 1D Motion / Kinematics
Vectors, Scalars, & Displacement
Learn with other creators
Practice this topic
- Multiple Choice
Starting from a pillar, you run a distance 140m east (the + x-direction), then turn around.
(a) How far west would you have to walk so that your total distance traveled is 300m?
(b) What is the magnitude and direction of your total displacement?
4043views168rank8comments - Multiple ChoiceThe figure shows two vectors. Which choice best represents ?1422views3rank
- Multiple ChoiceSeen from above, Linda runs 30° north of east. What is the x component of her velocity?1034views
- Multiple ChoiceIf , , and , what is ?1401views
- Textbook Question
Draw a pictorial representation for the following problem. Do not solve the problem. What acceleration does a rocket need to reach a speed of 200 m/s at a height of 1.0 km?
1408views - Textbook Question
Problems 49, 50, 51, and 52 show a partial motion diagram. For each: Draw a pictorial representation for your problem.
1123views - Textbook Question
Problems 44, 45, 46, 47, and 48 show a motion diagram. For each of these problems, write a one or two sentence 'story' about a real object that has this motion diagram. Your stories should talk about people or objects by name and say what they are doing.
1693views - Textbook Question
For Problems 34, 35, 36, 37, 38, 39, 40, 41, 42, and 43, draw a complete pictorial representation. Do not solve these problems or do any mathematics. A car starts from rest at a stop sign. It accelerates at 4.0 m/s² for 6.0 s, coasts for 2.0 s, and then slows at a rate of 2.5 m/s² for the next stop sign. How far apart are the stop signs?
1555views