Here are the essential concepts you must grasp in order to answer the question correctly.
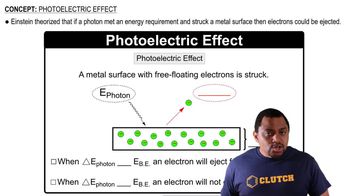
Photoelectric Effect
The photoelectric effect is the phenomenon where electrons are emitted from a material when it absorbs light of sufficient energy. The energy of the incoming light is determined by its wavelength, with shorter wavelengths corresponding to higher energy. This concept is crucial for understanding how light interacts with metals and the conditions under which electrons can be ejected.
Recommended video:
Work Function
The work function is the minimum energy required to remove an electron from the surface of a material. For cesium, this value is 188 kJ/mol, which translates to a specific wavelength of light that can provide enough energy to overcome this barrier. Understanding the work function helps determine whether a given wavelength of light will result in electron ejection.
Recommended video:
Work Function Calculation Example
Amplitude of Light Waves
The amplitude of a light wave relates to its intensity or brightness, but it does not affect the energy of individual photons. In the context of the photoelectric effect, while higher amplitude can increase the number of photons hitting the surface, it does not change the energy of each photon. Therefore, the amplitude alone does not determine whether electrons will be ejected, but rather the wavelength and energy of the light are the critical factors.
Recommended video: