Here are the essential concepts you must grasp in order to answer the question correctly.
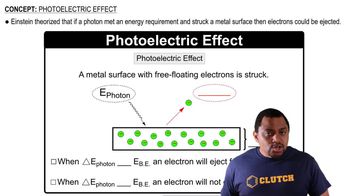
Photoelectric Effect
The photoelectric effect is the phenomenon where electrons are emitted from a material when it absorbs light of sufficient energy. This effect demonstrates the particle nature of light, where photons collide with electrons, providing them enough energy to overcome the material's work function, which is the minimum energy required to eject an electron.
Recommended video:
Energy and Wavelength Relationship
The energy of a photon is inversely related to its wavelength, described by the equation E = hc/λ, where E is energy, h is Planck's constant, c is the speed of light, and λ is the wavelength. This relationship indicates that shorter wavelengths correspond to higher energy photons, which is crucial for understanding how light can cause electron ejection in the photoelectric effect.
Recommended video:
Frequency-Wavelength Relationship
Conversion of Energy Units
In this context, energy is given in kJ/mol, which must be converted to joules per photon for calculations involving individual photons. Since 1 kJ = 1000 J and 1 mol contains Avogadro's number of particles (approximately 6.022 x 10^23), converting kJ/mol to J/photon allows for the application of the energy-wavelength relationship to find the corresponding wavelength of light.
Recommended video: