Some watch dials are coated with a phosphor, like ZnS, and a polymer in which some of the 1H atoms have been replaced by 3H atoms, tritium. The phosphor emits light when struck by the beta particle from the tritium decay, causing the dials to glow in the dark. The half-life of tritium is 12.3 yr. If the light given off is assumed to be directly proportional to the amount of tritium, by how much will a dial be dimmed in a watch that is 50 yr old?
The cloth shroud from around a mummy is found to have a 14C activity of 9.7 disintegrations per minute per gram of carbon as compared with living organisms that undergo 16.3 disintegrations per minute per gram of carbon. From the half-life for 14C decay, 5715 yr, calculate the age of the shroud.

Verified Solution
Key Concepts
Radiocarbon Dating
Half-Life

Disintegration Rate
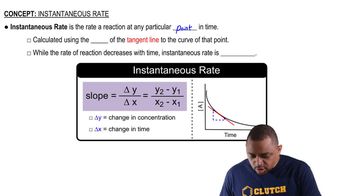
It takes 4 h 39 min for a 2.00-mg sample of radium-230 to decay to 0.25 mg. What is the half-life of radium-230?
Cobalt-60 is a strong gamma emitter that has a half-life of 5.26 yr. The cobalt-60 in a radiotherapy unit must be replaced when its radioactivity falls to 75% of the original sample. If an original sample was purchased in June 2016, when will it be necessary to replace the cobalt-60?
Potassium-40 decays to argon-40 with a half-life of 1.27 * 109 yr. What is the age of a rock in which the mass ratio of 40Ar to 40K is 4.2?
The thermite reaction, Fe2O31s2 + 2 Al1s2 ¡2 Fe1s2 + Al2O31s2, H = -851.5 kJ>mol, is one of the most exothermic reactions known. Because the heat released is sufficient to melt the iron product, the reaction is used to weld metal under the ocean. How much heat is released per mole of Al2O3 produced? How does this amount of thermal energy compare with the energy released when 2 mol of protons and 2 mol of neutrons combine to form 1 mol of alpha particles?
How much energy must be supplied to break a single aluminum-27 nucleus into separated protons and neutrons if an aluminum-27 atom has a mass of 26.9815386 amu? How much energy is required for 100.0 g of aluminum-27? (The mass of an electron is given on the inside back cover.)
