Here are the essential concepts you must grasp in order to answer the question correctly.
Ion-Product Constant (Kw)
The ion-product constant, Kw, is the equilibrium constant for the self-ionization of water, defined as Kw = [H+][OH-]. In pure water, this value is typically 1.0 x 10^-14 at 25 °C, but it can vary with temperature and the solvent used. For deuterium oxide (D2O), the ion-product constant is different due to the presence of deuterium, which affects the dissociation of the solvent.
Recommended video:
Solubility Product Constant
Concentration of Ions in Neutral Solutions
In a neutral solution, the concentrations of hydrogen ions [H+] and hydroxide ions [OH-] are equal. For deuterium oxide, the concentrations of deuterium ions (D+) and deuteroxide ions (OD-) will also be equal in a neutral solution. This means that if Kw is known, the concentration of each ion can be calculated using the equation [D+] = [OD-] = √Kw.
Recommended video:
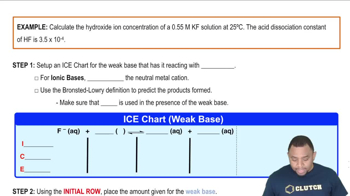
Hydroxide Ion Concentration Example
Temperature Effects on Ionization
Temperature influences the ionization of water and its isotopes. As temperature increases, the ion-product constant Kw typically increases, leading to higher concentrations of ions in solution. In the case of D2O at 20 °C, understanding how temperature affects Kw is crucial for accurately calculating the concentrations of D+ and OD- ions in neutral D2O.
Recommended video:
 Verified step by step guidance
Verified step by step guidance