Ch.14 - Chemical Kinetics

Problem 87b

Previous problem

Next problem

Chapter 14, Problem 87b

The activation energy of an uncatalyzed reaction is 95 kJ/mol. The addition of a catalyst lowers the activation energy to 55 kJ/mol. Assuming that the collision factor remains the same, by what factor will the catalyst increase the rate of the reaction at (b) 125 °C?

Verified step by step guidance

Convert the temperature from Celsius to Kelvin by adding 273.15 to the given temperature.

Use the Arrhenius equation: k = A * e^(-Ea/RT), where k is the rate constant, A is the collision factor, Ea is the activation energy, R is the gas constant (8.314 J/mol·K), and T is the temperature in Kelvin.

Calculate the rate constant for the uncatalyzed reaction using the activation energy of 95 kJ/mol.

Calculate the rate constant for the catalyzed reaction using the activation energy of 55 kJ/mol.

Determine the factor by which the catalyst increases the rate by dividing the rate constant of the catalyzed reaction by the rate constant of the uncatalyzed reaction.

Verified Solution

Video duration:

This video solution was recommended by our tutors as helpful for the problem above.

Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Activation Energy

Activation energy is the minimum energy required for a chemical reaction to occur. It represents the energy barrier that reactants must overcome to form products. A higher activation energy means that fewer molecules have sufficient energy to react, resulting in a slower reaction rate. Conversely, lowering the activation energy, such as through the use of a catalyst, increases the likelihood of successful collisions between reactant molecules.

Catalysts

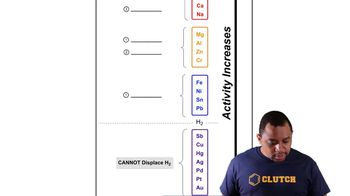
Catalysts are substances that increase the rate of a chemical reaction without being consumed in the process. They work by providing an alternative reaction pathway with a lower activation energy. This allows more reactant molecules to have enough energy to collide and react, thereby speeding up the reaction. Importantly, catalysts do not alter the equilibrium position of a reaction; they only affect the rate at which equilibrium is reached.

Arrhenius Equation

The Arrhenius equation describes how the rate constant of a reaction depends on temperature and activation energy. It is expressed as k = A * e^(-Ea/RT), where k is the rate constant, A is the pre-exponential factor, Ea is the activation energy, R is the gas constant, and T is the temperature in Kelvin. This equation illustrates that as the activation energy decreases or the temperature increases, the rate constant increases, leading to a faster reaction rate.

Recommended video:

Arrhenius Equation

Related Practice

The enzyme carbonic anhydrase catalyzes the reaction CO2(g) + H2O(l) ↔ HCO3⁻(aq) + H⁺(aq). In water, without the enzyme, the reaction proceeds with a rate constant of 0.039 s⁻¹ at 25 _x001E_C. In the presence of the enzyme in water, the reaction proceeds with a rate constant of 1.0 * 10⁶ s⁻¹ at 25 _x001E_C. Assuming the collision factor is the same for both situations, calculate the difference in activation energies for the uncatalyzed versus enzyme-catalyzed reaction.

Textbook Question

The enzyme urease catalyzes the reaction of urea, 1NH2CONH22, with water to produce carbon dioxide and ammonia. In water, without the enzyme, the reaction proceeds with a first-order rate constant of 4.15 * 10-5 s-1 at 100 C. In the presence of the enzyme in water, the reaction proceeds with a rate constant of 3.4 * 104 s-1 at 21 C. (c) In actuality, what would you expect for the rate of the catalyzed reaction at 100 C as compared to that at 21 C?

2128

views

Textbook Question

The activation energy of an uncatalyzed reaction is 95 kJ/mol. The addition of a catalyst lowers the activation energy to 55 kJ/mol. Assuming that the collision factor remains the same, by what factor will the catalyst increase the rate of the reaction at (a) 25 C

Suppose that a certain biologically important reaction is quite slow at physiological temperature 137 _x001E_C2 in the absence of a catalyst. Assuming that the collision factor remains the same, by how much must an enzyme lower the activation energy of the reaction to achieve a 1 * 10^5-fold increase in the reaction rate?

Textbook Question

Consider the reaction A + B → C + D. Is each of the following statements true or false? (b) If the reaction is an elementary reaction, the rate law is second order.

373

views

Textbook Question

Consider the reaction A + B → C + D. Is each of the following statements true or false? (c) If the reaction is an elementary reaction, the rate law of the reverse reaction is first order.

775

views