Energy bands are considered continuous due to the large number of closely spaced energy levels. The range of energy levels in a crystal of copper is approximately 1 * 10–19 J. Assuming equal spacing between levels, the spacing between energy levels may be approximated by dividing the range of energies by the number of atoms in the crystal. (b) Determine the average spacing in J between energy levels in the copper metal in part (a).

Key Concepts

Energy Bands

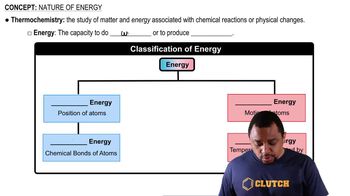
Energy bands in solids arise from the overlap of atomic orbitals in a crystal lattice, leading to a continuum of energy levels. In metals like copper, these bands allow for the conduction of electricity as electrons can move freely between closely spaced energy levels. Understanding energy bands is crucial for analyzing the electrical and thermal properties of materials.

Energy Level Spacing

The spacing between energy levels in a solid can be approximated by dividing the total range of energy levels by the number of available states, which is often related to the number of atoms in the crystal. This concept is essential for determining how energy is quantized in a material and influences its electronic properties, such as conductivity and band gap.

Crystal Structure

The arrangement of atoms in a crystal structure significantly affects its physical properties, including energy levels and band formation. In metals like copper, the face-centered cubic (FCC) structure allows for a high density of atoms, contributing to the close spacing of energy levels. Understanding crystal structure is vital for predicting how materials will behave under various conditions.