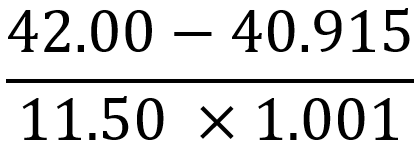Significant Figures: In Calculations - Online Tutor, Practice Problems & Exam Prep

In chemistry calculations, the precision of your final answer is guided by the rules of significant figures. When multiplying or dividing, your result should have the same number of significant figures as the measurement with the fewest significant figures. For example, if you multiply 3.16 (three significant figures) by 0.307 (three significant figures) and by $5.7\times {10}^{-3}$ (two significant figures), your final answer should have two significant figures, reflecting the least precise measurement.

In contrast, when adding or subtracting, the result should have the same number of decimal places as the least precise measurement. For instance, if you subtract 2.9 (one decimal place) from 12.2 (one decimal place) and add 2.671 (three decimal places), your final answer should have one decimal place.

When calculations involve a mix of operations, follow the order of operations (parentheses, exponents, multiplication/division, addition/subtraction) and apply the rules of significant figures at each step. Multiplication and division dictate the number of significant figures, while addition and subtraction control the number of decimal places in the final answer.

Significant Figures Calculations Concept 1

So now we're going to see how significant figures can be incorporated in different calculations that will be exposed to in chemistry. Now we're going to start out with multiplication and division. We're going to say when either multiplying or dividing different numbers, the final answer will contain the least significant figures.

And if we take a look at this example, it says perform the following calculation to the right number of sig figs. Here we have three values that are being multiplied together. We have 3.16 ∗ 0.003027 ∗ 5.7 ∗ 10 - 3. We just said that when you're multiplying or dividing its least number of sig figs for your final answer. So we need to determine the number of sig figs for each value.

From our topic on significant figures we know that if we have a decimal point which all are going to do, we move from left to right. Now remember we're going to start counting once we get to our first non 0 number. Here 3 is our first non 0 number and once we start counting we count all the way into the end, so 123. This has three sigfix for the next one skip, skip, skip. Our first non 0 is this 3 1234. This has four sig figs and then finally we have 5.7 ∗ 10 - 3 written in scientific notation.

Remember when it's written in scientific notation? Just focus on the coefficient. We're going to say our first non 0 number is this 5, and once we start counting we count all the way into the end, so 1-2. This has two sig figs. Now, based on our sig figs of 3-4 and two, we have to go with the least number of significant figures. That means our answer at the end can only have two significant figures.

So when we first get our answer, what we see initially is 5.4522324 ∗ 10 - 5. We want two sig figs here. That four that we have though, we look to the right of it and see if we either keep it as four or we round U next to it. We have this long string of numbers and we have a 5 there. Because that number is five. That means we have to round up so the 5.4 becomes now 5.5 and then times 10 - 5.

This represents our answer, which has the least number of significant figures based on the initial values given. We were given these three numbers initially, and the one with the least number of sig figs was the one written in scientific notation. So that tells me that my final answer has to have that number of significant figures. Now that we've looked at multiplication and division, let's go on to our next video and let's see what happens when we incorporate addition and subtraction.

Significant Figures Calculations Concept 2

Now when either adding or subtracting different numbers, the final answer will contain the least decimal places. If we take a look at this example, it says perform the following calculation to the right number of sig figs. Now if our answer is based on the least number of decimal places, that's going to have a direct impact on the number of significant figures.

If we take a look here, it says we have four O 2.09 -, 2.12 + 2.671. If we look at these values, this one has 2 decimal places. This one here has one decimal place, and this one here has three decimal places. Based on that, we're going with the least number of decimal places. Our answer can only have one decimal place at the end.

When we punch all this in, we get 192.561. We can only have one decimal place to the right of that five. There's a six there. That means we have to round up. So this is 182.6 as our final answer. And if you wanted to talk about the number of sig figs, you'd move from left to right. Our first non 0 number is this one and counting all the way through. We'd have four sig figs at the end.

By following this least number of decimal places, it has a direct impact on the number of sig figs in our final answer. Up to this point, we've kept multiplication and division separate from addition and subtraction, but what happens when you mix them together? To find out what to do, click on the next video.

Significant Figures Calculations Concept 3

Now we're dealing with mixed operations, where we have a combination of multiplication, divisions, subtraction, or addition, we're going to say. When dealing with this mixture of multiplication, division, addition, and subtraction, we must follow the order of operations. To help us remember the order of operations, we'll use PEMDAS, which stands for parentheses. So what's in parentheses is done first? Exponents or powers? Then we have multiplication, division and then addition slash subtraction. So that is our order of operations.

Multiplication and division are grouped together. Addition and subtraction are still grouped together. If we take a look here, it says perform the following calculation to the right number of sig figs we have in brackets 1.89×106×3.005. Then we have 5.213÷8.829-6.5+2.920. All right, so we're following our order of operations, and in our order of operations, we're going to do what's in here? First, because we have brackets in parentheses here, so we're going to say when we do everything inside of here. When we multiply everything, it comes out to 567-9450.

But when you're multiplying or dividing numbers, we have to look at the least number of sig figs. So here this number has three sig figs. This number here has four sigfigs. So our answer at the end when they multiply has to have three sig figs. So this initial answer that I got here becomes 5.68×106 after I've changed it into scientific notation. Next we have 5.213, so that's exponent. So all this means is 5.21×5.21×5.21. All of them are multiplying each other. All of them have three sig figs. What we would get initially from it is 141.420761, but again when you're multiplying its least number of sig figs. So our answer would have to have three sig figs. So here this will come out to be 141.

Next we have what's on the bottom here, 8.29-6.5 if you're adding or subtracting its least number of decimal places. So what we would get initially is 2.329 when we subtract. But this number here has three decimal places. This one here has one decimal place. So our answer at the end must have one decimal place, so that will come out to be 2.3 as our number here. Next we have +2.920. So we're looking at this portion down here. Now we continue onward. Now the two numbers on the top are multiplying each other, because they're multiplying it still least sig figs. Here the coefficient has three sig figs, and here 141. Oops, going the other way because it doesn't have a decimal place, 141 has three sig figs. So our answer at the end must have three sig figs. When they multiply together, it comes out as 8.01×108.

Notice I'm not putting everything all at once in my calculator. You have to do a piece by piece in order to isolate your final answer. Then on the bottom these two are adding together O. When they add together initially it comes out as 5.220. But when you're adding or subtracting its least number of decimal places, this one here has one, this one here has three. So your answer at the end must have one decimal place, so that would be 5.2. Now we just have these two numbers that are dividing each other. So again it's least number of sig figs. This 8.01 has three sig figs in it. This 5.2 has two sig figs in it, So our answer at the end must have two sig figs. So this comes out as 15×108.

So this would be our final answer written to the correct number of significant figure based on this mix of operations. So just keep in mind the order of operations to guide you on what to do. And remember multiplication and division is least sig figs addition or subtraction is least decimal places.

Perform the following calculation to the right number of sig figs:

[(1.7 × 10⁶) ÷ (2.63 × 10⁵)] + 6.96

• A. 13.46
• B. 13.0
• C. 13.5
• D. 14.2
• E. 4.471

What answer should be reported, with the correct number of significant figures, for the following calculation?

• A. 0.00822
• B. 0.0845
• C. 0.0921
• D. 0.0947

Here’s what students ask on this topic:

Which of the following is a rule of significant figures in calculations?

When performing calculations with measurements, the rules of significant figures (or significant digits) ensure that the precision of the result is consistent with the precision of the data used in the calculation. Here's a key rule to remember:

1. Multiplication and Division: When you multiply or divide numbers, the result should have as many significant figures as the number with the fewest significant figures used in the calculation. For example, if you multiply 3.12 (3 significant figures) by 2.1 (2 significant figures), your result should be reported with 2 significant figures.
2. Addition and Subtraction: When you add or subtract numbers, the result should have the same number of decimal places as the number with the fewest decimal places. For instance, if you add 12.11 (2 decimal places) to 3.1 (1 decimal place), your result should be reported with 1 decimal place.

Always round off the final result appropriately based on these rules to ensure that you are not overestimating the precision of your calculated values.

How many significant figures are proper in the results of the following calculations?

To determine the number of significant figures in the results of calculations, you need to follow specific rules depending on the operation:

1. Addition and Subtraction: The result should have the same number of decimal places as the measurement with the least number of decimal places. For example, if you add 12.11 (two decimal places) and 3.1 (one decimal place), your result should be rounded to one decimal place.
2. Multiplication and Division: The result should have the same number of significant figures as the measurement with the least number of significant figures. For example, if you multiply 2.5 (two significant figures) by 3.42 (three significant figures), your result should be rounded to two significant figures.

Remember, when performing multiple operations, apply these rules sequentially after each step to maintain accuracy. Non-zero digits are always significant, and zeros can be significant depending on their position and whether there is a decimal point present.

How do you use significant figures in calculations?

When using significant figures in calculations, it's important to follow some basic rules to ensure accuracy and precision. Here's a concise guide:

1. Addition/Subtraction: When adding or subtracting, your answer should have the same number of decimal places as the measurement with the least number of decimal places. For example, if you add 12.345 (3 decimal places) to 7.8 (1 decimal place), your answer should be rounded to 1 decimal place.
2. Multiplication/Division: For these operations, your answer should have the same number of significant figures as the measurement with the least number of significant figures. If you multiply 123 (3 significant figures) by 4.56 (3 significant figures), your answer should be reported with 3 significant figures.
3. Mixed Operations: If your calculation involves a mix of addition/subtraction and multiplication/division, apply the rules in sequence for each operation. Calculate in the order indicated by the parentheses or other mathematical conventions, applying the significant figures rules at each step.
4. Exact Numbers: Numbers that are counted (like 25 students) or defined (like 1 inch equals 2.54 cm) are considered exact and do not limit the number of significant figures in your final answer.

Remember, the purpose of significant figures is to communicate how precise your measurements are.