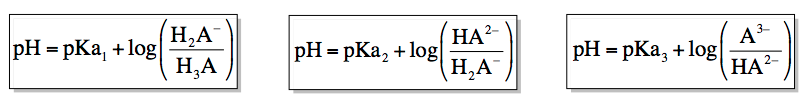Polyprotic Buffers - Online Tutor, Practice Problems & Exam Prep

Polyprotic buffers, often triprotic, contain three acidic hydrogens and have three corresponding acid dissociation constants (pKa values). The Henderson-Hasselbalch equation varies based on the form of the buffer: for the acid form to the first intermediate, it is $pH=\mathrm{pKa}+\log (\mathrm{intermediate\; 1}/\mathrm{acid\; form})$. Understanding these relationships is crucial for calculating pH in polyprotic systems, such as citric acid.

Polyprotic Buffers

So with our discussion of monoprotic buffers, diprotic buffers, we're now left with polyprotic buffers. Here, we're going to say polyprotic buffers usually is synonymous with a triprotic buffer where we have 3 acidic hydrogens. We're going to say here a triprotic buffer can be approached in a way similar to diprotic buffers. The key difference is that a triprotic acid has now 3 pKa values or 3 Ka values. Again, when we say polyprotic, we're usually referring to triprotic acids, but there are acids with more than 3 acidic hydrogens. Those are fewer, so we tend to just stick to 3 acidic hydrogens. Now we're going to say for polyprotic buffers, remember we have different forms that our polyprotic acid can take. We have the fully acidified version or its fully protonated version which is H₃A. Here, it has all 3 of its acidic hydrogens. We can talk about removing the 1st acidic hydrogen. If we're talking about removing the 1st acidic hydrogen, that means we're talking about Ka₁. Removing that first acidic hydrogen gives us our first intermediate form which is H₂A^-. Then we remove the 2nd acidic hydrogen giving us Ka₂ involved. Now we get the 2nd intermediate form which is HA₂^-. Then finally, we're removing the last acidic hydrogen which will give us our basic form A₃^3-. Remember in earlier videos where we talked about polyprotic acids in general, if we could talk about Ka going one way in removing acidic hydrogen, we could talk about Kb when adding back acidic hydrogens. Remember here, this would be Kb₁, this would be Kb₂, and this would be Kb₃. If you don't quite remember that, make sure you go back and take a look at our polyprotic acid videos. We talk about the relationships between your acid dissociation constants and your base dissociation constants when looking at protic, diprotic, and polyprotic acids.

Now with these different forms of our polyprotic buffers, we have different forms of the Henderson-Hasselbalch equation. In this first one here, we're talking about the relationship between the acid form and the 1st intermediate form, then we know we're dealing with Ka₁. And so the equation is pH equals pKa₁ plus log of the intermediate one over the acid form. Remember, the bottom portion of the Henderson-Hasselbalch equation is the portion that contains more acidic H⁺ ions. And the top version, which represents the more basic form, has one less acidic H⁺ ion. Then if we're talking about our second form of the Henderson-Hasselbalch equation, we're talking about pKa₂ which means we're talking about the relationship between our first intermediate and the second intermediate. We've removed the second acidic hydrogen, so that's Ka₂ which is why we're dealing with pKa₂. Here it would be plus log of intermediate 2 divided by intermediate 1. Again, the more acidic form, the one with more hydrogens goes on the bottom. The one that is more basic, the one that has less acidic H⁺ ions goes on top. Then finally, in this form, we're talking about intermediate 2 going to the basic form. So we're dealing with Ka₃. Just as before, we put the more acidic form on the bottom and the more basic form on top.

Now here, we could take a common example, citric acid. Citric acid represents a triprotic acid, so it has 3 acidic hydrogens. In these three different scenarios, in this first one, we have 0.10 molar of citric acid. Then we have 0.15 molar of the 1st intermediate form. Here, it's lost one of its acidic hydrogens and it's been replaced by a sodium ion here. Since we're talking about the acid form and the 1st intermediate form, we're dealing with Ka₁. Here, this would be pH equals pKa₁ plus log of the conjugate base form which is 0.15 molar divided by 0.10 molar. That'd be negative log of 7.4 times 10^-4 plus log of 1.5 which would give us 3.31 as our pH at the end. For the next form, here we're dealing with moles. Remember, in the Henderson-Hasselbalch equation, we can plug in molarity or moles into these areas. In the first one, we had molarity for both, so we plugged in molarity. Now we have moles, so we'll plug in the moles now. Here, this would be pH equals negative log of 1.7 times 10^-5 plus log of the more basic form goes on top, the one with less acidic hydrogens which would be this one on top. So 0.25 moles divided by the more acidic form, the one with more H⁺ ions on the bottom. Here, that would give me 4.94 at the end. Then finally, here we have volume of molarity. Remember in this last situation, moles equals liters times molarity. If you divide these mL's by 1,000, you'll get their liters. Then you just multiply by their molarities. Right? So you'd get 0.016 moles. And then we have 0.060 liters times 0.25 molar. And then give us 0.015 moles. So pH here equals negative log of Ka₃ times 10^-7 plus log of more basic moles on top divided by the more acidic moles on the bottom. At the end, that will give us 6.43. Just remember, when we're dealing with a polyprotic buffer, it is important that you know which forms we are dealing with in the question. This will dictate if you're going to use Ka₁, Ka₂, or Ka₃ in terms of the Henderson-Hasselbalch equation. As we delve deeper and deeper into these different types of buffers, always keep this in mind.

Here’s what students ask on this topic:

What is a polyprotic buffer and how does it differ from monoprotic and diprotic buffers?

A polyprotic buffer contains multiple acidic hydrogens, typically three, and is often referred to as a triprotic buffer. This means it has three acid dissociation constants (pKa values). In contrast, a monoprotic buffer has only one acidic hydrogen and one pKa value, while a diprotic buffer has two acidic hydrogens and two pKa values. The key difference lies in the number of dissociation steps and the corresponding pKa values, which affect the buffer's ability to resist changes in pH at different stages of hydrogen ion removal.

How do you use the Henderson-Hasselbalch equation for polyprotic buffers?

The Henderson-Hasselbalch equation for polyprotic buffers varies based on the form of the buffer. For the acid form to the first intermediate, the equation is:

$\mathrm{pH}={\mathrm{pK}}_1+\frac{\log ({\mathrm{intermediate}}_1/\mathrm{acid})}{}$

For the first intermediate to the second intermediate, it is:

$\mathrm{pH}={\mathrm{pK}}_2+\frac{\log ({\mathrm{intermediate}}_2/{\mathrm{intermediate}}_1)}{}$

For the second intermediate to the basic form, it is:

$\mathrm{pH}={\mathrm{pK}}_3+\frac{\log (\mathrm{basic}/{\mathrm{intermediate}}_2)}{}$

Understanding which form you are dealing with is crucial for accurate pH calculation.

What are some common examples of polyprotic acids used in buffers?

Common examples of polyprotic acids used in buffers include citric acid, phosphoric acid, and sulfuric acid. Citric acid is a triprotic acid with three acidic hydrogens and three corresponding pKa values. Phosphoric acid is another triprotic acid commonly used in biological systems and industrial applications. Sulfuric acid, although a strong acid, can also act as a polyprotic acid with two dissociation steps. These acids are used in various buffer systems to maintain pH stability across different pH ranges.

How do you calculate the pH of a polyprotic buffer solution?

To calculate the pH of a polyprotic buffer solution, you need to identify the specific form of the buffer you are dealing with. Use the appropriate Henderson-Hasselbalch equation based on the dissociation step:

1. For the acid form to the first intermediate: $\mathrm{pH}={\mathrm{pK}}_1+\frac{\log ({\mathrm{intermediate}}_1/\mathrm{acid})}{}$

2. For the first intermediate to the second intermediate: $\mathrm{pH}={\mathrm{pK}}_2+\frac{\log ({\mathrm{intermediate}}_2/{\mathrm{intermediate}}_1)}{}$

3. For the second intermediate to the basic form: $\mathrm{pH}={\mathrm{pK}}_3+\frac{\log (\mathrm{basic}/{\mathrm{intermediate}}_2)}{}$

Plug in the concentrations or moles of the relevant species to find the pH.

Why is it important to understand the different forms of polyprotic acids in buffer solutions?

Understanding the different forms of polyprotic acids in buffer solutions is crucial because each form has a different pKa value and thus a different buffering capacity. Knowing which form you are dealing with allows you to use the correct Henderson-Hasselbalch equation to calculate the pH accurately. This is essential for applications in chemistry, biology, and medicine where precise pH control is necessary. Additionally, understanding these forms helps in predicting how the buffer will respond to the addition of acids or bases, ensuring effective pH stabilization.