In Exercises 5–18, the unit circle has been divided into twelve equal arcs, corresponding to t-values of
0, 𝜋, 𝜋, 𝜋, 2𝜋, 5𝜋, 𝜋, 7𝜋, 4𝜋, 3𝜋, 5𝜋, 11𝜋, and 2𝜋.
6 3 2 3 6 6 3 2 3 6
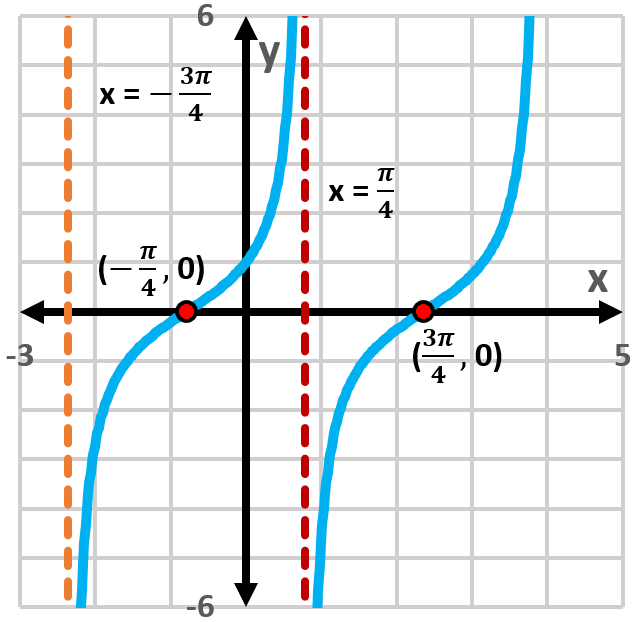
Use the (x,y) coordinates in the figure to find the value of each trigonometric function at the indicated real number, t, or state that the expression is undefined.
<IMAGE>
In Exercises 11–18, continue to refer to the figure at the bottom of the previous page.
sec 11𝜋/6