 Back
Back- In Exercises 1–4, the graph of a tangent function is given. Select the equation for each graph from the following options: y = tan(x + π/2), y = tan(x + π), y = −tan(x − π/2).
Problem 1
Problem 1.1
A point P(x, y) is shown on the unit circle corresponding to a real number t. Find the values of the trigonometric functions at t.
<IMAGE>
Problem 1.11
In Exercises 5–18, the unit circle has been divided into twelve equal arcs, corresponding to t-values of
0, 𝜋, 𝜋, 𝜋, 2𝜋, 5𝜋, 𝜋, 7𝜋, 4𝜋, 3𝜋, 5𝜋, 11𝜋, and 2𝜋.
6 3 2 3 6 6 3 2 3 6
Use the (x,y) coordinates in the figure to find the value of each trigonometric function at the indicated real number, t, or state that the expression is undefined.
<IMAGE>
In Exercises 11–18, continue to refer to the figure at the bottom of the previous page.
csc 7𝜋/6
Problem 1.12
Use the given triangles to evaluate each expression. If necessary, express the value without a square root in the denominator by rationalizing the denominator.
<IMAGE>
csc 45°
Problem 1.13
Use the given triangles to evaluate each expression. If necessary, express the value without a square root in the denominator by rationalizing the denominator.
<IMAGE>
tan 𝜋/3
Problem 1.15
The unit circle has been divided into twelve equal arcs, corresponding to t-values of
0, 𝜋/6, 𝜋/3, 𝜋/2, 2𝜋/3, 5𝜋/6, 𝜋, 7𝜋/6, 4𝜋/3, 3𝜋/2, 5𝜋/3, 11𝜋/6, and 2𝜋
Use the (x,y) coordinates in the figure to find the value of each trigonometric function at the indicated real number, t, or state that the expression is undefined.
<IMAGE>
sin 3𝜋/2
Problem 1.17
In Exercises 5–18, the unit circle has been divided into twelve equal arcs, corresponding to t-values of
0, 𝜋, 𝜋, 𝜋, 2𝜋, 5𝜋, 𝜋, 7𝜋, 4𝜋, 3𝜋, 5𝜋, 11𝜋, and 2𝜋.
6 3 2 3 6 6 3 2 3 6
Use the (x,y) coordinates in the figure to find the value of each trigonometric function at the indicated real number, t, or state that the expression is undefined.
<IMAGE>
In Exercises 11–18, continue to refer to the figure at the bottom of the previous page.
sec 3𝜋/2
Problem 1.19a
Use the unit circle shown to find the value of the trigonometric function.
cos 𝜋/6
Problem 1.22a
Use the unit circle shown to find the value of the trigonometric function.
sin (2𝜋/3)
Problem 1.24a
Use the unit circle shown to find the value of the trigonometric function.
tan 11𝜋/6
Problem 1.25a
The unit circle has been divided into eight equal arcs, corresponding to t-values of
0, 𝜋/4, 𝜋/2, 3𝜋/4, 𝜋, 5𝜋/4, 3𝜋/2, 7𝜋/4, and 2𝜋.
a. Use the (x,y) coordinates in the figure to find the value of the trigonometric function.
b. Use periodic properties and your answer from part (a) to find the value of the same trigonometric function at the indicated real number.
<IMAGE>
sin 3𝜋/4
Problem 1.29
Find a cofunction with the same value as the given expression.
cos (𝜋/2)
Problem 1.3
A point P(x, y) is shown on the unit circle corresponding to a real number t. Find the values of the trigonometric functions at t.
<IMAGE>
Problem 1.37
Find the reference angle for each angle.
205°
Problem 1.38
Find a cofunction with the same value as the given expression.
cos (3𝜋/8)
Problem 1.4.13
In Exercises 5–18, the unit circle has been divided into twelve equal arcs, corresponding to t-values of
0, 𝜋, 𝜋, 𝜋, 2𝜋, 5𝜋, 𝜋, 7𝜋, 4𝜋, 3𝜋, 5𝜋, 11𝜋, and 2𝜋.
6 3 2 3 6 6 3 2 3 6
Use the (x,y) coordinates in the figure to find the value of each trigonometric function at the indicated real number, t, or state that the expression is undefined.
<IMAGE>
In Exercises 11–18, continue to refer to the figure at the bottom of the previous page.
sec 11𝜋/6
Problem 1.5
The unit circle has been divided into twelve equal arcs, corresponding to t-values of
0, 𝜋/6, 𝜋/3, 𝜋/2, 2𝜋/3, 5𝜋/6, 𝜋, 7𝜋/6, 4𝜋/3, 3𝜋/2, 5𝜋/3, 11𝜋/6, and 2𝜋
Use the (x,y) coordinates in the figure to find the value of each trigonometric function at the indicated real number, t, or state that the expression is undefined.
<IMAGE>
sin 𝜋/6
Problem 1.55
Find the reference angle for each angle.
23π/4
- In Exercises 1–4, a point P(x, y) is shown on the unit circle corresponding to a real number t. Find the values of the trigonometric functions at t.
Problem 2
- In Exercises 1–4, the graph of a tangent function is given. Select the equation for each graph from the following options: y = tan(x + π/2), y = tan(x + π), y = −tan(x − π/2).
Problem 3

- In Exercises 1–4, graph one period of each function. y = 2 tan x/2
Problem 3
- In Exercises 1–4, a point P(x, y) is shown on the unit circle corresponding to a real number t. Find the values of the trigonometric functions at t.
Problem 4
Problem 5
In Exercises 1–8, use the given vectors to find v⋅w and v⋅v. v = -6i - 5j, w = -10i - 8j
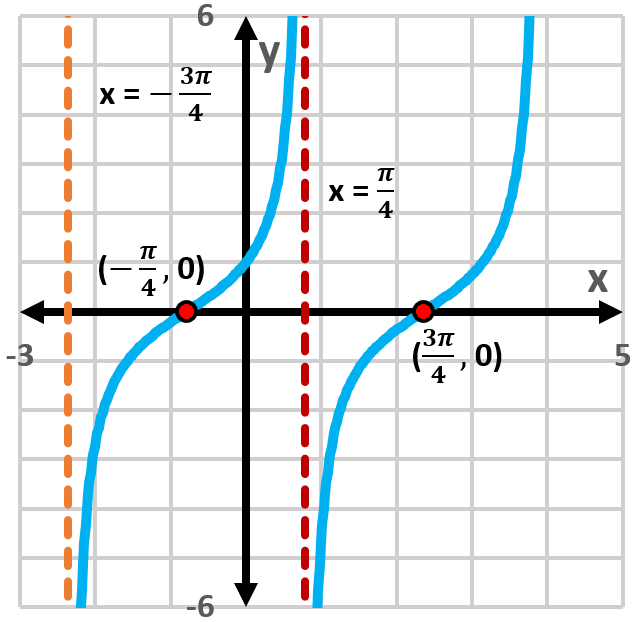
- In Exercises 5–12, graph two periods of the given tangent function. y = 3 tan x/4
Problem 5
- In Exercises 5–18, the unit circle has been divided into twelve equal arcs, corresponding to t-values of 0, 𝜋, 𝜋, 𝜋, 2𝜋, 5𝜋, 𝜋, 7𝜋, 4𝜋, 3𝜋, 5𝜋, 11𝜋, and 2𝜋. 6 3 2 3 6 6 3 2 3 6 Use the (x,y) coordinates in the figure to find the value of each trigonometric function at the indicated real number, t, or state that the expression is undefined. sin 𝜋/3
Problem 6
Problem 7
The unit circle has been divided into twelve equal arcs, corresponding to t-values of
0, 𝜋/6, 𝜋/3, 𝜋/2, 2𝜋/3, 5𝜋/6, 𝜋, 7𝜋/6, 4𝜋/3, 3𝜋/2, 5𝜋/3, 11𝜋/6, and 2𝜋
Use the (x,y) coordinates in the figure to find the value of each trigonometric function at the indicated real number, t, or state that the expression is undefined.
<IMAGE>
cos 5𝜋/6
- In Exercises 5–18, the unit circle has been divided into twelve equal arcs, corresponding to t-values of 0, 𝜋, 𝜋, 𝜋, 2𝜋, 5𝜋, 𝜋, 7𝜋, 4𝜋, 3𝜋, 5𝜋, 11𝜋, and 2𝜋. 6 3 2 3 6 6 3 2 3 6 Use the (x,y) coordinates in the figure to find the value of each trigonometric function at the indicated real number, t, or state that the expression is undefined.
Problem 8
cos 2𝜋/3
- In Exercises 5–12, graph two periods of the given tangent function. y = −2 tan 1/2 x
Problem 9
- In Exercises 5–18, the unit circle has been divided into twelve equal arcs, corresponding to t-values of 0, 𝜋, 𝜋, 𝜋, 2𝜋, 5𝜋, 𝜋, 7𝜋, 4𝜋, 3𝜋, 5𝜋, 11𝜋, and 2𝜋. 6 3 2 3 6 6 3 2 3 6 Use the (x,y) coordinates in the figure to find the value of each trigonometric function at the indicated real number, t, or state that the expression is undefined.
Problem 10
tan 0
Problem 11
Use the given triangles to evaluate each expression. If necessary, express the value without a square root in the denominator by rationalizing the denominator.
<IMAGE>
sec 45°
