Light enters a solid pipe made of plastic having an index of refraction of 1.60. The light travels parallel to the upper part of the pipe (Fig. E33.15). You want to cut the face AB so that all the light will reflect back into the pipe after it first strikes that face. (b) If the pipe is immersed in water of refractive index 1.33, what is the largest that u can be?

Verified step by step guidance

1. Identify the critical angle for total internal reflection at the interface between the plastic pipe and water. Use the formula for the critical angle, \( \theta_c = \sin^{-1}(\frac{n_2}{n_1}) \), where \( n_1 \) is the refractive index of the plastic (1.60) and \( n_2 \) is the refractive index of water (1.33).
2. Calculate the critical angle using the values provided. This angle represents the maximum angle at which light can strike the interface and still be totally internally reflected.
3. Understand that the angle \( u \) in the problem is the angle of incidence inside the plastic pipe, relative to the normal at the interface. For total internal reflection to occur, \( u \) must be greater than or equal to the critical angle.
4. Set up the inequality \( u \geq \theta_c \) to find the range of possible values for \( u \).
5. Interpret the result to determine the largest possible value for \( u \) that ensures all light reflects back into the pipe when it strikes face AB.

Key Concepts

Index of Refraction

The index of refraction is a dimensionless number that describes how light propagates through a medium. It is defined as the ratio of the speed of light in a vacuum to the speed of light in the medium. A higher index indicates that light travels slower in that medium, affecting how light bends when entering or exiting different materials.

Total Internal Reflection

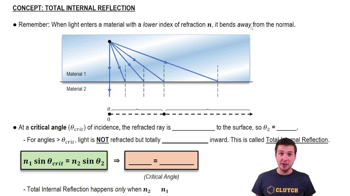
Total internal reflection occurs when a light wave traveling in a medium hits a boundary with a less dense medium at an angle greater than the critical angle. Instead of refracting, the light is completely reflected back into the denser medium. This phenomenon is crucial for applications like fiber optics and is dependent on the indices of refraction of the two media involved.

Critical Angle

The critical angle is the minimum angle of incidence at which total internal reflection occurs. It can be calculated using the formula sin(θc) = n2/n1, where θc is the critical angle, n1 is the index of refraction of the denser medium, and n2 is that of the less dense medium. Understanding the critical angle is essential for determining the conditions under which light will reflect rather than refract at a boundary.