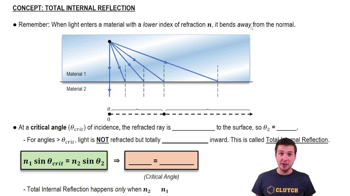
Textbook Question
Light of original intensity I0 passes through two ideal polarizing filters having their polarizing axes oriented as shown in Fig. E33.28. You want to adjust the angle f so that the intensity at point P is equal to I0/10. (a) If the original light is unpolarized, what should Φ be?
383
views