A long, straight solenoid has 800 turns. When the current in the solenoid is 2.90 A, the average flux through each turn of the solenoid is 3.25 * 10^-3 Wb. What must be the magnitude of the rate of change of the current in order for the self-induced emf to equal 6.20 mV?

Verified step by step guidance

1. Identify the given values: number of turns (N) = 800, current (I) = 2.90 A, magnetic flux per turn (\( \Phi \)) = 3.25 * 10^-3 Wb, and desired emf (\( \mathcal{E} \)) = 6.20 mV.
2. Recall the formula for the self-induced emf in a solenoid, which is given by \( \mathcal{E} = -N \frac{d\Phi}{dt} \). Here, \( \frac{d\Phi}{dt} \) is the rate of change of magnetic flux.
3. Since the flux linkage (\( \Phi_{total} \)) is the product of the number of turns and the flux per turn, calculate \( \Phi_{total} = N \times \Phi \).
4. Rearrange the emf formula to solve for \( \frac{d\Phi}{dt} \): \( \frac{d\Phi}{dt} = -\frac{\mathcal{E}}{N} \).
5. Substitute the values of \( \mathcal{E} \) and N into the equation to find \( \frac{d\Phi}{dt} \), which represents the required rate of change of the magnetic flux.

Key Concepts

Self-Induced EMF

Self-induced electromotive force (emf) occurs in a coil when the current flowing through it changes, generating a magnetic field that induces an emf opposing the change. This phenomenon is described by Faraday's law of electromagnetic induction, which states that the induced emf is proportional to the rate of change of magnetic flux through the coil.

Faraday's Law of Induction

Faraday's Law quantifies how a changing magnetic field within a closed loop induces an emf. The law states that the induced emf (ε) is equal to the negative rate of change of magnetic flux (Φ) through the loop, expressed mathematically as ε = -dΦ/dt. This principle is fundamental in understanding how solenoids and inductors operate in circuits.

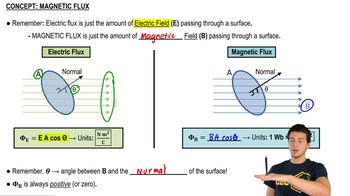
Magnetic Flux

Magnetic flux (Φ) is a measure of the quantity of magnetism, taking into account the strength and the extent of a magnetic field. It is defined as the product of the magnetic field (B) and the area (A) through which the field lines pass, adjusted for the angle (θ) between the field lines and the normal to the surface: Φ = B * A * cos(θ). In the context of solenoids, it helps determine the amount of magnetic field produced by the current.