Heat Q flows into a monatomic ideal gas, and the volume increases while the pressure is kept constant. What fraction of the heat energy is used to do the expansion work of the gas?

Verified step by step guidance

1. Identify the first law of thermodynamics, which states that the change in internal energy of a system (\(\Delta U\)) is equal to the heat added to the system (Q) minus the work done by the system (W): \(\Delta U = Q - W\).
2. Recognize that for an ideal gas undergoing a process at constant pressure, the work done by the gas during expansion can be calculated using the formula \(W = P \Delta V\), where \(P\) is the pressure and \(\Delta V\) is the change in volume.
3. Understand that the change in internal energy (\(\Delta U\)) for a monatomic ideal gas can be expressed in terms of the number of moles (n), the gas constant (R), and the change in temperature (\(\Delta T\)) as \(\Delta U = \frac{3}{2} nR\Delta T\).
4. Combine the first law of thermodynamics with the expressions for work and internal energy to relate the heat added to the system: \(Q = \Delta U + W = \frac{3}{2} nR\Delta T + P\Delta V\).
5. To find the fraction of the heat energy used to do the expansion work, calculate the ratio of the work done by the gas to the total heat added: \(\text{Fraction} = \frac{W}{Q} = \frac{P\Delta V}{\frac{3}{2} nR\Delta T + P\Delta V}\). This fraction represents how much of the heat energy is converted into work during the expansion.

Key Concepts

First Law of Thermodynamics

The First Law of Thermodynamics states that energy cannot be created or destroyed, only transformed. In the context of heat transfer into a system, the law can be expressed as ΔU = Q - W, where ΔU is the change in internal energy, Q is the heat added to the system, and W is the work done by the system. This principle is essential for understanding how heat energy is converted into work during the expansion of the gas.

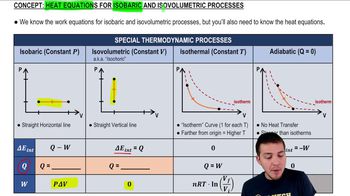
Isobaric Process

An isobaric process is a thermodynamic process that occurs at constant pressure. In this scenario, as heat is added to the monatomic ideal gas, it expands while maintaining constant pressure. The work done by the gas during this expansion can be calculated using the formula W = PΔV, where P is the pressure and ΔV is the change in volume, highlighting the relationship between heat, work, and volume change.

Monatomic Ideal Gas

A monatomic ideal gas consists of single atoms and follows the ideal gas law, which relates pressure, volume, and temperature (PV = nRT). For monatomic gases, the specific heat capacities are well-defined, with the molar specific heat at constant pressure (C_p) being higher than that at constant volume (C_v). Understanding the properties of monatomic ideal gases is crucial for calculating the fraction of heat energy used for work during the expansion process.