A gas undergoes two processes. In the first, the volume remains constant at $0.200$ m³ and the pressure increases from $2.00 imes10^5$ Pa to $5.00 imes10^5$ Pa. The second process is a compression to a volume of $0.120$ m³ at a constant pressure of $5.00 imes10^5$ Pa. In a $p V$ -diagram, show both processes.

Question

Accepted Answer

Hey everyone today. We're dealing with the problem about pressure versus volume graphs. So we're being given a two step process where during the first step the gas has a fixed volume of 0.5 m cubed as its pressures increase from one times 10 to the fifth pascal's to 4.25 times 10 to the fifth pascal's increased in the second step, the volume is reduced 2 0.3 - five m cubed But the pressure is kept constant at 4.25 times 10 to the 5th Pascal's. So with this information we're being asked to sketch the entire process. Excuse me, on a pressure versus volume diagram. So in a pressure versus volume diagram let's write this out. Pressure will be on the y axis while the volume will be on the X axis. So here's pressure and volume and then increasing in the positive Y. And positive X directions respectfully. So let's mark this point right here as 0. m. Cute. This is the origin. Let's put this as 0.325 m cubed. And then I'll just put this in 10 to the fifth pascal's. Um But this will be let's just keep this at one times 10 to the fifth pascal's and this is 4.25 times 10 to the fifth pascal's. So this in mind, let's start with step one. So step one says that the volume is kept constant And the pressure is increased from one 2 4.25 times 10 to the 5th Pascal's. So we're starting here And let's do step one in blue. So we're starting here. And since the volume is kept constant we'll have a vertical line but the pressure is increasing from 1 to 4.25 times 10 to the fifth pascal's. So we'll have a vertical line shot a little better. We'll have a vertical line all the way up to 4.25. So that's step one. Now with the red we'll do step two we're being told that the volume is then reduced to 0.3 to five m cubed and the pressure is kept constant at 4.25 times 10 to the fifth pascal's so the pressure is not changing the pressure then stays at this level here but it's decreased. The volume has decreased from 0.5 m cubed 20.3 to 5 m cubed. So it goes this way. So this is what our graph rpV graph our PV diagram will look like. And the only one that matches this is anti choice. See I hope this helps. And I look forward to seeing you all in the next one

Verified video answer for a similar problem:

Key Concepts

Pressure-Volume (pV) Diagram

Isovolumetric Process

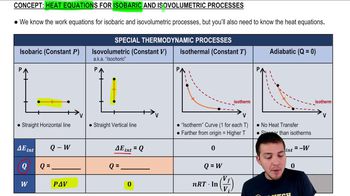
Isobaric Process