Here are the essential concepts you must grasp in order to answer the question correctly.
Specific Heat Capacity
Specific heat capacity is the amount of heat required to change the temperature of a unit mass of a substance by one degree Celsius. For water, this value is approximately 4.18 J/g°C. In this problem, it is essential to calculate the heat removed to lower the temperature of the water from 18.0°C to 0.0°C before freezing.
Recommended video:
Specific Heat & Temperature Changes
Heat of Fusion
The heat of fusion is the amount of energy required to change a substance from a solid to a liquid at its melting point, or vice versa. For water, the heat of fusion is about 334 J/g. This concept is crucial for determining the energy needed to freeze the water after it has been cooled to 0.0°C.
Recommended video:
Overview of Heat Transfer
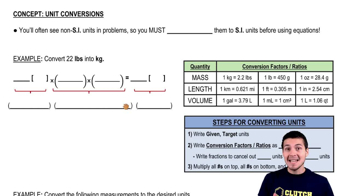
Units of Energy
Energy can be expressed in various units, including joules (J), calories (cal), and British thermal units (Btu). Understanding these units is important for converting the calculated heat energy into the required formats. For instance, 1 cal is approximately 4.184 J, and 1 Btu is about 252 cal, which will be necessary for the final answer.
Recommended video: