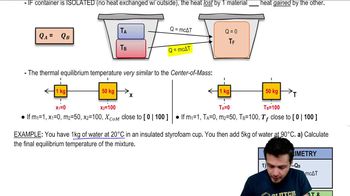
Textbook Question
A copper pot with a mass of 0.500 kg contains 0.170 kg of water, and both are at 20.0°C. A 0.250-kg block of iron at 85.0°C is dropped into the pot. Find the final temperature of the system, assuming no heat loss to the surroundings.
1197
views