Two uniform spheres, each with mass M and radius R, touch each other. What is the magnitude of their gravitational force of attraction?

Verified step by step guidance

1. Identify the formula for the gravitational force between two masses. The formula is given by Newton's law of universal gravitation: F = G \frac{m_1 m_2}{r^2}, where F is the gravitational force, G is the gravitational constant, m_1 and m_2 are the masses of the objects, and r is the distance between the centers of the two masses.
2. Substitute the values for m_1 and m_2 with M, since both spheres have the same mass M.
3. Determine the distance r between the centers of the two spheres. Since the spheres touch each other and each has a radius R, the distance between their centers is r = 2R.
4. Substitute r = 2R into the gravitational force formula. This modifies the formula to F = G \frac{M^2}{(2R)^2}.
5. Simplify the expression to find the formula for the gravitational force in terms of G, M, and R. The simplified formula becomes F = G \frac{M^2}{4R^2}.

Key Concepts

Newton's Law of Universal Gravitation

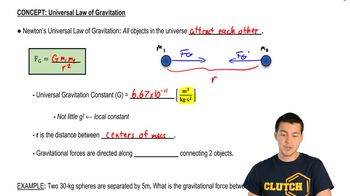
This law states that every point mass attracts every other point mass with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centers. The formula is given by F = G(m1*m2)/r^2, where F is the gravitational force, G is the gravitational constant, m1 and m2 are the masses, and r is the distance between the centers of the two masses.

Gravitational Constant (G)

The gravitational constant, denoted as G, is a fundamental physical constant used in the calculation of gravitational forces. Its approximate value is 6.674 × 10^-11 N(m/kg)^2. This constant is crucial for quantifying the strength of the gravitational force between two masses, regardless of their size or distance apart.

Distance Between Centers of Mass

In the context of two touching spheres, the distance between their centers is equal to the sum of their radii. For two spheres of radius R, this distance is 2R. This distance is essential for calculating the gravitational force using Newton's law, as it directly influences the force's magnitude through the inverse square relationship.