Here are the essential concepts you must grasp in order to answer the question correctly.
Hydrostatic Pressure
Hydrostatic pressure is the pressure exerted by a fluid at equilibrium due to the force of gravity. It increases with depth in a fluid, calculated using the formula P = ρgh, where P is pressure, ρ is the fluid density, g is the acceleration due to gravity, and h is the depth. In the context of the Challenger Deep, the immense depth results in significantly high pressure on the water.
Recommended video:
Pressure and Atmospheric Pressure
Bulk Modulus
The bulk modulus (k) is a measure of a substance's resistance to uniform compression. It quantifies how much a material's volume decreases under pressure, defined as the ratio of pressure increase to the relative decrease in volume. For seawater, the bulk modulus is essential for calculating the change in volume when subjected to the high pressures found at great depths.
Recommended video:
Volume Change Calculation
The change in volume of a substance under pressure can be calculated using the formula ΔV = -V0(P - P0)/k, where ΔV is the change in volume, V0 is the original volume, P is the final pressure, P0 is the initial pressure, and k is the bulk modulus. This relationship allows us to determine how much a cubic meter of seawater will compress when taken from the surface to the depths of the ocean.
Recommended video:
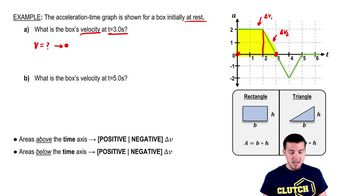
Calculating Change in Velocity from Acceleration-Time Graphs
 Verified step by step guidance
Verified step by step guidance